题目内容
1.表是二次函数y=ax2+bx+c的部分x,y的对应值:| x | … | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | m | $\frac{1}{4}$ | -1 | $-\frac{7}{4}$ | -2 | $-\frac{7}{4}$ | -1 | $\frac{1}{4}$ | 2 | … |
(2)当x>0时,y的取值范围是y≥-2;
(3)当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时,n的取值范围是n>-3.
分析 (1)由表中所给x、y的对应值,可求得二次函数解析式,可求得抛物线的开口方向及顶点坐标,令x=-1代入可求得m的值;
(2)由二次函数的解析式可求得其增减性,当x>0时,可知其有最小值,无最大值,可求得y的取值范围;
(3)在y=x+n中,令x=1代入,结合条件可得到关于n的不等式,可求得n的取值范围.
解答 解:
(1)把点(0,-1),(1,-2)和(2,-1)代入二次函数解析式可得
$\left\{\begin{array}{l}{c=-1}\\{a+b+c=-2}\\{4a+2b+c=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-1}\end{array}\right.$,
∴二次函数解析式为y=x2-2x-1=(x-1)2-2,
∴二次函数图象开口向上,顶点坐标为(1,-2),
令x=-1,代入可得m=2,
故答案为:上;(1,-2);2;
(2)∵y=(x-1)2-2,
∴当x=1时,y有最小值-2,
∴当x>0时,y≥-2,
故答案为:y≥-2;
(3)在y=x+n中,令x=1代入可得y=1+n,
∵抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时,
∴1+n>-2,解得n>-3,
故答案为:n>-3.
点评 本题主要考查二次函数的性质,利用待定系数法求得二次函数解析式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
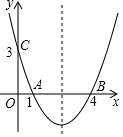 如图,抛物线y=ax2+bx+c经过A(1,0),B(4,0),C(0,3)三点,求抛物线的解析式.
如图,抛物线y=ax2+bx+c经过A(1,0),B(4,0),C(0,3)三点,求抛物线的解析式. 如图,△ABC内接于⊙O,∠C=45°,半径OB的长为3,则AB的长为3$\sqrt{2}$.
如图,△ABC内接于⊙O,∠C=45°,半径OB的长为3,则AB的长为3$\sqrt{2}$.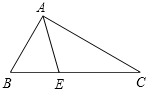 如图,在△ABC中,已知∠B=60°,∠C=30°,AE是△ABC角平分线,求:∠BEA的度数.
如图,在△ABC中,已知∠B=60°,∠C=30°,AE是△ABC角平分线,求:∠BEA的度数.