题目内容
15．若等腰三角形的顶角为30°，则一腰上的高与底边所成的角的度数是15度．分析 根据等腰三角形的性质和三角形内角和定理可求出等腰三角形的底角的度数，然后在一腰上的高与底边所构成的直角三角形中，可得出所求角的度数．
解答 
解：如图：△ABC中，AB=AC，BD是边AC上的高．
∵∠A=30°，且AB=AC，
∴∠ABC=∠C=（180°-30°）÷2=75°；
在Rt△BDC中，
∠BDC=90°，∠C=75°；
∴∠DBC=90°-75°=15°．
故答案为15．
点评 本题主要考查等腰三角形的性质，掌握等腰三角形两底角相等和三角形内角和定理是解题的关键．
练习册系列答案
一本好题口算题卡系列答案
相关题目
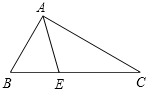如图，在△ABC中，已知∠B=60°，∠C=30°，AE是△ABC角平分线，求：∠BEA的度数．
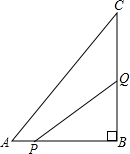如图，在△ABC中，∠B=90°，AB=3厘米，BC=4厘米，点P从A沿AB边向点B以1厘米/秒的速度移动，点Q从B沿BC边向点C以2厘米/秒的速度移动，如P与Q同时出发，且当一点移动到端点并停止时，另一点也同时停下，1秒或2秒后三角形PBQ的面积为2平方厘米．
3．某校2016年给希望工程捐款2万，以后每年都捐款，计划到2018年三年总共捐款6.62万元．若设该校捐款的年平均增长率为x，则可列方程为（ ）
| A． | 2+2×2（1+x）=6.62 | B． | 2（1+x）2=6.62 | ||
| C． | 2+2（1+x）+2（1+x）2=6.62 | D． | 2（1+x）（1+2x）=6.62 |
如图，AB是半圆的直径，点C、D是半圆上两点，∠ABC=40°，则∠ADC=140°．