题目内容
14. 如图所示,△ABC中,DE∥FG∥BC,且AD=DF=FB,则S△AFG:S△ABC=4:9.
如图所示,△ABC中,DE∥FG∥BC,且AD=DF=FB,则S△AFG:S△ABC=4:9.
分析 先根据题意得出△AFG∽△ABC,相似比为2:6,再由相似三角形的性质即可得出结论.
解答 解:∵△ABC中,DE∥FG∥BC,且AD=DF=FB,
∴△AFG∽△ABC,
∴$\frac{AF}{AB}$=$\frac{2}{3}$,
∴S△AFG:S△ABC=($\frac{2}{3}$)2=4:9.
故答案为:4:9.
点评 本题考查的是相似三角形的判定与性质,熟知相似三角形面积的比等于相似比的平方是解答此题的关键.

练习册系列答案
相关题目
3.某校2016年给希望工程捐款2万,以后每年都捐款,计划到2018年三年总共捐款6.62万元.若设该校捐款的年平均增长率为x,则可列方程为( )
| A. | 2+2×2(1+x)=6.62 | B. | 2(1+x)2=6.62 | ||
| C. | 2+2(1+x)+2(1+x)2=6.62 | D. | 2(1+x)(1+2x)=6.62 |
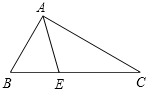 如图,在△ABC中,已知∠B=60°,∠C=30°,AE是△ABC角平分线,求:∠BEA的度数.
如图,在△ABC中,已知∠B=60°,∠C=30°,AE是△ABC角平分线,求:∠BEA的度数.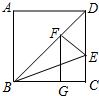 如图,在矩形ABCD中,已知∠DBC=45°,∠DBC的平分线交DC于点E,作EF⊥BD于点F,作FG⊥BC于点G,则$\frac{BG}{GC}$=$\sqrt{2}$+1.
如图,在矩形ABCD中,已知∠DBC=45°,∠DBC的平分线交DC于点E,作EF⊥BD于点F,作FG⊥BC于点G,则$\frac{BG}{GC}$=$\sqrt{2}$+1.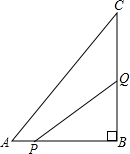 如图,在△ABC中,∠B=90°,AB=3厘米,BC=4厘米,点P从A沿AB边向点B以1厘米/秒的速度移动,点Q从B沿BC边向点C以2厘米/秒的速度移动,如P与Q同时出发,且当一点移动到端点并停止时,另一点也同时停下,1秒或2秒后三角形PBQ的面积为2平方厘米.
如图,在△ABC中,∠B=90°,AB=3厘米,BC=4厘米,点P从A沿AB边向点B以1厘米/秒的速度移动,点Q从B沿BC边向点C以2厘米/秒的速度移动,如P与Q同时出发,且当一点移动到端点并停止时,另一点也同时停下,1秒或2秒后三角形PBQ的面积为2平方厘米.