题目内容
6.请写出一个二次函数y=ax2+bx+c.满足:(1)图象的对称轴为直线x=1;
(2)x=2时,y>0;x=-2时,y<0.
分析 先作图象满足抛物线对称轴为直线x=1,若抛物线经过点(-1,0)和(3,0),则满足x=2时,y>0;x=-2时,y<0.然后令a=1,用交点式可写出满足条件的抛物线解析式.
解答 解:如图, 设抛物线经过点(-1,0)和(3,0),
设抛物线经过点(-1,0)和(3,0),
设抛物线解析式为y=a(x+1)(x-3),
若a=1,
则抛物线解析式为y=-x2+2x+3.
点评 本题考查了抛物线与x轴的交点:通过解关于x的一元二次方程ax2+bx+c=0(a,b,c是常数,a≠0)得到二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,△ABC内接于⊙O,∠C=45°,半径OB的长为3,则AB的长为3$\sqrt{2}$.
如图,△ABC内接于⊙O,∠C=45°,半径OB的长为3,则AB的长为3$\sqrt{2}$. .
.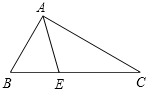 如图,在△ABC中,已知∠B=60°,∠C=30°,AE是△ABC角平分线,求:∠BEA的度数.
如图,在△ABC中,已知∠B=60°,∠C=30°,AE是△ABC角平分线,求:∠BEA的度数.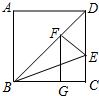 如图,在矩形ABCD中,已知∠DBC=45°,∠DBC的平分线交DC于点E,作EF⊥BD于点F,作FG⊥BC于点G,则$\frac{BG}{GC}$=$\sqrt{2}$+1.
如图,在矩形ABCD中,已知∠DBC=45°,∠DBC的平分线交DC于点E,作EF⊥BD于点F,作FG⊥BC于点G,则$\frac{BG}{GC}$=$\sqrt{2}$+1.