题目内容
19. 如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-1,3)、B(n,-1).
如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-1,3)、B(n,-1).(1)求反比例函数的解析式;
(2)当y1>y2时,直接写出x的取值范围.
分析 (1)把A点坐标代入${y_2}=\frac{m}{x}$可求出m的值,从而得到反比例函数解析式;
(2)利用反比例函数解析式确定B点坐标,然后观察函数图象,写出一次函数图象在反比例函数图象上方所对应的自变量的取值范围即可.
解答 解:(1)把A(-1,3)代入${y_2}=\frac{m}{x}$可得m=-1×3=-3,
所以反比例函数解析式为y=-$\frac{3}{x}$;
(2)把B(n,-1)代入y=-$\frac{3}{x}$得-n=-3,解得n=3,则B(3,-1),
所以当x<-1或0<x<3,y1>y2.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
9.若抛物线y=x2-bx+9的顶点在x轴的负半轴上,则b的值为( )
| A. | ±3 | B. | 6 | C. | -6 | D. | ±6 |
7.下列说法中,正确的是( )
| A. | $\sqrt{25}$=±5 | B. | -42的平方根是±4 | ||
| C. | 64的立方根是±4 | D. | 0.01的算术平方根是0.1 |
4. 如图,小将同学将一个直角三角形的纸片折叠,A与B重合,折痕为DE,若已知AC=4,BC=3,∠C=90°,则EC的长为( )
如图,小将同学将一个直角三角形的纸片折叠,A与B重合,折痕为DE,若已知AC=4,BC=3,∠C=90°,则EC的长为( )
 如图,小将同学将一个直角三角形的纸片折叠,A与B重合,折痕为DE,若已知AC=4,BC=3,∠C=90°,则EC的长为( )
如图,小将同学将一个直角三角形的纸片折叠,A与B重合,折痕为DE,若已知AC=4,BC=3,∠C=90°,则EC的长为( )| A. | $\frac{8}{7}$ | B. | $\frac{7}{8}$ | C. | 2 | D. | $\frac{3}{4}$ |
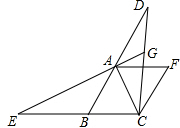 如图,在?ABCF中,∠ABC=60°,AB=BC,延长BA到D,延长CB到E,使BE=AD,连结DC,交AF于H,连结EA并延长交CD于点G.
如图,在?ABCF中,∠ABC=60°,AB=BC,延长BA到D,延长CB到E,使BE=AD,连结DC,交AF于H,连结EA并延长交CD于点G. 如图,在长为32米,宽为20米的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上小草.要使草坪的面积为540平方米,则道路的宽为2米.
如图,在长为32米,宽为20米的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上小草.要使草坪的面积为540平方米,则道路的宽为2米.