题目内容
9．若抛物线y=x2-bx+9的顶点在x轴的负半轴上，则b的值为（ ）| A． | ±3 | B． | 6 | C． | -6 | D． | ±6 |
分析 抛物线y=ax2+bx+c的顶点坐标为（-$\frac{b}{2a}$，$\frac{4ac-{b}^{2}}{4a}$），因为抛物线y=x2-bx+9的顶点在x轴上，所以顶点的横坐标小于0，纵坐标为零，列不等式和方程求解．
解答 解：∵抛物线y=x2-bx+9的顶点在x轴的负半轴上，
∴顶点的横坐标小于0，纵坐标为零，即x=-$\frac{-b}{2×1}$＜0，y=$\frac{4ac-{b}^{2}}{4a}$=$\frac{36-{b}^{2}}{4}$=0，解得b=-6，
故选C．
点评 此题考查了二次函数的性质，解题的关键是掌握顶点的表示方法和x轴上的点的特点．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
在平面直角坐标系中，已知两点A（1，2），B（-1，-1），若△ABC是以线段AB为一腰，对称轴平行于y轴的等腰三角形，则C点的坐标是（3，-1）或（-3，2）．
4．
下列几何体的截面是（ ）
下列几何体的截面是（ ）| A． |  | B． |  | C． |  | D． |  |
14．
在下列网格中，小正方形的边长为1，点A、B、O都在格点上，则∠A的正弦值是（ ）
在下列网格中，小正方形的边长为1，点A、B、O都在格点上，则∠A的正弦值是（ ）| A． | $\frac{\sqrt{5}}{5}$ | B． | $\frac{\sqrt{5}}{10}$ | C． | $\frac{2\sqrt{5}}{5}$ | D． | $\frac{1}{2}$ |
1．
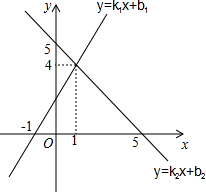已知函数y=k1x+b1与函数y=k2x+b2的图象如图所示，则方程组$\left\{\begin{array}{l}{{k}_{1}x+{b}_{1}-y=0}\\{{k}_{2}x+{b}_{2}-y=0}\end{array}\right.$的解为（ ）
已知函数y=k1x+b1与函数y=k2x+b2的图象如图所示，则方程组$\left\{\begin{array}{l}{{k}_{1}x+{b}_{1}-y=0}\\{{k}_{2}x+{b}_{2}-y=0}\end{array}\right.$的解为（ ）| A． | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=-1}\\{y=5}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=5}\\{y=5}\end{array}\right.$ |
18．已知点（-3，y1），（1，y2）都在直线y=kx+2（k＜0）上，则y1，y2大小关系是（ ）
| A． | y1＞y2 | B． | y1=y2 | C． | y1＜y2 | D． | 不能比较 |
如图，一次函数y1=-x+2的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A（-1，3）、B（n，-1）．