题目内容
11.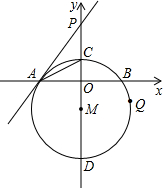 如图,在直角坐标系中,⊙M的圆心M在y轴上,⊙M与x轴交于点A、B,与y轴交于点C、D,过点A作⊙M的切线AP交y轴于点P,若⊙M的半径为5,点A的坐标为(-4,0),
如图,在直角坐标系中,⊙M的圆心M在y轴上,⊙M与x轴交于点A、B,与y轴交于点C、D,过点A作⊙M的切线AP交y轴于点P,若⊙M的半径为5,点A的坐标为(-4,0),(1)求证:∠PAC=∠CAO;
(2)求直线PA的解析式;
(3)若点Q为⊙M上任意一点,连接OQ、PQ,问$\frac{OQ}{PQ}$的比值是否发生变化?若不变求出此值;若变化,说明变化规律.
分析 (1)连接MA,如图1,易证∠PAC=∠OAC,要求tan∠PAC的值,只需求tan∠OAC的值,只需求出OA、OC即可;
(2)如图1,由于点A的坐标已知,要求直线PA的解析式,只需求出点P的坐标,只需求出OP的长,易证△AOM∽△PAM,根据相似三角形的性质可求出MP,从而可求出OP,问题得以解决;
(3)连接MQ,如图2,由于MA=MQ,结合(2)中已证的结论,由此可证到△MOQ∽△MQP,然后运用相似三角形的性质即可解决问题.
解答 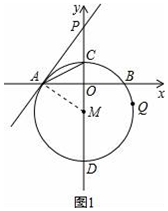 解:(1)连接MA,如图1,
解:(1)连接MA,如图1,
∵PA是⊙M的切线,
∴AM⊥AP,
∴∠PAC+∠MAC=90°,
∵MA=MC,
∴∠MCA=∠MAC,
∵∠OAC+∠MCA=90°,
∴∠PAC=∠OAC;
(2)如图1,
∵∠AMO=∠PMA,∠AOM=∠PAM=90°,
∴△AOM∽△PAM,
∴$\frac{MA}{MP}$=$\frac{MO}{MA}$,
∴MA2=MO•MP.
在Rt△AOM中,
∵AO=4,AM=5,∴OM=3.
∴25=3MP,
∴MP=$\frac{25}{3}$,
∴OP=MP-OM=$\frac{25}{3}$-3=$\frac{16}{3}$,
∴点P的坐标为(0,$\frac{16}{3}$),
设直线PA的解析式为y=kx+b,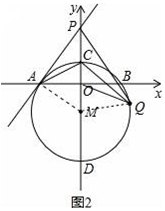
则有$\left\{\begin{array}{l}{-4k+b=0}\\{b=\frac{16}{3}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=\frac{16}{3}}\end{array}\right.$,
∴直线PA的解析式为y=$\frac{4}{3}$x+$\frac{16}{3}$;
(3)连接MQ,如图2,
∵$\frac{MA}{MP}=\frac{MO}{MA}$((2)中已证),MA=MQ,
∴$\frac{MQ}{MP}=\frac{MC}{MQ}$,
∵∠QMO=∠PMQ,
∴△MOQ∽△MQP,
∴$\frac{OQ}{PQ}$=$\frac{MO}{MQ}$=$\frac{3}{5}$,
∴$\frac{OQ}{PQ}$不变,等于$\frac{3}{5}$.
点评 本题主要考查了切线的性质、相似三角形的判定与性质、运用待定系数法求直线的解析式、锐角三角函数的定义、勾股定理等知识,有一定的综合性.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{600}{x}=\frac{600}{(1+20%)x}-2$ | B. | $\frac{600}{x}=\frac{600}{(1+20%)x}+2$ | ||
| C. | $\frac{600}{x}=\frac{600}{20%x}-2$ | D. | $\frac{600}{x}+2=\frac{600}{(1+20%)x}$ |
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
| A. | a2•a3=a6 | B. | (-2xy2)3=-8x3y5 | C. | 2a-3=$\frac{1}{2{a}^{3}}$ | D. | (-a)3÷(2a)2=-$\frac{1}{4}$a |
 如图,矩形ABCD的对角线相交于点O,AB=4cm,∠AOB=60°,则AC=8cm.
如图,矩形ABCD的对角线相交于点O,AB=4cm,∠AOB=60°,则AC=8cm.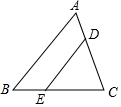 如图所示,△ABC中,点D、E分别是AC、BC边上的点,且DE∥AB,CD:CA﹦2:3,△ABC的面积是18,则四边形ABED的面积是( )
如图所示,△ABC中,点D、E分别是AC、BC边上的点,且DE∥AB,CD:CA﹦2:3,△ABC的面积是18,则四边形ABED的面积是( )