题目内容
1.某学校为绿化环境,计划种植600棵树,实际劳动中每小时植树的数量比原计划多20%,结果提前2小时完成任务,设原计划每小时植树x棵,则列出的方程为( )| A. | $\frac{600}{x}=\frac{600}{(1+20%)x}-2$ | B. | $\frac{600}{x}=\frac{600}{(1+20%)x}+2$ | ||
| C. | $\frac{600}{x}=\frac{600}{20%x}-2$ | D. | $\frac{600}{x}+2=\frac{600}{(1+20%)x}$ |
分析 设原计划每小时植树x棵,则实际劳动中每小时植树的数量是120%x棵,根据“结果提前2小时完成任务”列出方程即可.
解答 解:设原计划每小时植树x棵,
依题意得:$\frac{600}{x}$=$\frac{600}{(1+20%)x}$+2,
故选B.
点评 本题考查了由实际问题抽象出分式方程,解答本题的关键是设出未知数,找出合适的等量关系列方程.

练习册系列答案
相关题目
6. 如图,现给出下列条件:①∠1=∠2,②∠B=∠5,③∠3=∠4,④∠5=∠D,⑤∠B+∠BCD=180°,其中能够得到AD∥BC的条件是①④.(填序号)
如图,现给出下列条件:①∠1=∠2,②∠B=∠5,③∠3=∠4,④∠5=∠D,⑤∠B+∠BCD=180°,其中能够得到AD∥BC的条件是①④.(填序号)
能够得到AB∥CD的条件是②③⑤.(填序号)
 如图,现给出下列条件:①∠1=∠2,②∠B=∠5,③∠3=∠4,④∠5=∠D,⑤∠B+∠BCD=180°,其中能够得到AD∥BC的条件是①④.(填序号)
如图,现给出下列条件:①∠1=∠2,②∠B=∠5,③∠3=∠4,④∠5=∠D,⑤∠B+∠BCD=180°,其中能够得到AD∥BC的条件是①④.(填序号)能够得到AB∥CD的条件是②③⑤.(填序号)
10.已知直线y=kx+b,其中k+b=-5,kb=6,那么直线经过象限为( )
| A. | 第二、四 | B. | 第二、三、四 | C. | 第一、三 | D. | 第一、二、三 |
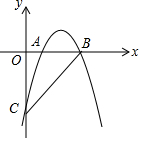 已知抛物线y=-x2+4x-3经过A(1,0),B(3,0),点C(0,-3),在抛物线上是否存在一点P,使得∠PCB>∠ACB,若存在,求出P点的横坐标的取值范围.
已知抛物线y=-x2+4x-3经过A(1,0),B(3,0),点C(0,-3),在抛物线上是否存在一点P,使得∠PCB>∠ACB,若存在,求出P点的横坐标的取值范围.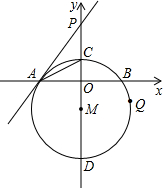 如图,在直角坐标系中,⊙M的圆心M在y轴上,⊙M与x轴交于点A、B,与y轴交于点C、D,过点A作⊙M的切线AP交y轴于点P,若⊙M的半径为5,点A的坐标为(-4,0),
如图,在直角坐标系中,⊙M的圆心M在y轴上,⊙M与x轴交于点A、B,与y轴交于点C、D,过点A作⊙M的切线AP交y轴于点P,若⊙M的半径为5,点A的坐标为(-4,0),