题目内容
6.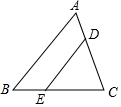 如图所示,△ABC中,点D、E分别是AC、BC边上的点,且DE∥AB,CD:CA﹦2:3,△ABC的面积是18,则四边形ABED的面积是( )
如图所示,△ABC中,点D、E分别是AC、BC边上的点,且DE∥AB,CD:CA﹦2:3,△ABC的面积是18,则四边形ABED的面积是( )| A. | 6 | B. | 8 | C. | 9 | D. | 10 |
分析 根据相似三角形的判定和性质即可得到结论.
解答 解:∵DE∥AB,
∴△CDE∽△CAB,
∴$\frac{{S}_{△CDE}}{{S}_{△CAB}}$=($\frac{CD}{CE}$)2=$\frac{4}{9}$,
∵△ABC的面积是18,
∴S△CDE=8,
∴四边形ABED的面积=18-8=10,
故选D.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.先化简:($\frac{x}{x-2}$-$\frac{4}{{x}^{2}-2x}$)÷$\frac{x+2}{{x}^{2}-x}$,然后从-2,-1,0,1,2中选取一个你喜欢的值代入求值.
15.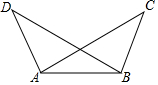 如图,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=5,BD=6,AD=4,那么BC等于( )
如图,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=5,BD=6,AD=4,那么BC等于( )
 如图,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=5,BD=6,AD=4,那么BC等于( )
如图,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=5,BD=6,AD=4,那么BC等于( )| A. | 4 | B. | 6 | C. | 5 | D. | 无法确定 |
16.已知一元二次方程x2-4x-3=0两根为m,n,则m2-mn+n2的值为( )
| A. | 25 | B. | 16 | C. | 9 | D. | 7 |
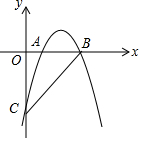 已知抛物线y=-x2+4x-3经过A(1,0),B(3,0),点C(0,-3),在抛物线上是否存在一点P,使得∠PCB>∠ACB,若存在,求出P点的横坐标的取值范围.
已知抛物线y=-x2+4x-3经过A(1,0),B(3,0),点C(0,-3),在抛物线上是否存在一点P,使得∠PCB>∠ACB,若存在,求出P点的横坐标的取值范围.
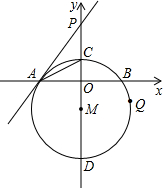 如图,在直角坐标系中,⊙M的圆心M在y轴上,⊙M与x轴交于点A、B,与y轴交于点C、D,过点A作⊙M的切线AP交y轴于点P,若⊙M的半径为5,点A的坐标为(-4,0),
如图,在直角坐标系中,⊙M的圆心M在y轴上,⊙M与x轴交于点A、B,与y轴交于点C、D,过点A作⊙M的切线AP交y轴于点P,若⊙M的半径为5,点A的坐标为(-4,0), 如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.
如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.