题目内容
已知y=(m-3)x-
是关于x的一次函数,且y随x的增大而增大.
(1)写山符合题意的3个m的值:
(2)设一次函数y=(m-3)x-
与x轴交于点A,与y轴交于点B,m为何值时△AOB的面积等于
.
| 1 |
| 3 |
(1)写山符合题意的3个m的值:
(2)设一次函数y=(m-3)x-
| 1 |
| 3 |
| 1 |
| 18 |
考点:一次函数图象上点的坐标特征,一次函数的定义
专题:
分析:(1)先根据y随x的增大而增大得出关于m的不等式,写出符合条件的m的值即可;
(2)先求A、B两点的坐标,根据三角形的面积公式求解即可.
(2)先求A、B两点的坐标,根据三角形的面积公式求解即可.
解答:解:(1)∵y随x的增大而增大,
∴m-3>0,即m>3,
∴m的值可以是4,5,6;
(2)∵当x=0时,y=-
;当y=0时,x=
,
∴A(
,0),B(0,-
),
∵m-3>0,
∴S△AOB=
×
×
=
,解得m=4,
∴当m=4时,△AOB的面积等于
.
∴m-3>0,即m>3,
∴m的值可以是4,5,6;
(2)∵当x=0时,y=-
| 1 |
| 3 |
| 1 |
| 3(m-3) |
∴A(
| 1 |
| 3(m-3) |
| 1 |
| 3 |
∵m-3>0,
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 3(m-3) |
| 1 |
| 3 |
| 1 |
| 18 |
∴当m=4时,△AOB的面积等于
| 1 |
| 18 |
点评:本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 如图,在矩形ABCD中,对角线AC,BD相交于点O,如果∠AOD=120°,AB=2,那么BC的长为( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,如果∠AOD=120°,AB=2,那么BC的长为( )| A、4 | ||
B、
| ||
C、2
| ||
D、2
|
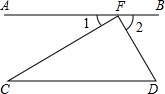 完成下面证明,并在下面括号里,填上推理的根据.
完成下面证明,并在下面括号里,填上推理的根据. 如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
 如图,在?ABCD中,E、F分别是AB,CD的中点,求证:DE=BF.
如图,在?ABCD中,E、F分别是AB,CD的中点,求证:DE=BF. 如图,某农场建一个矩形的养鸡场,鸡场的一边靠墙(墙长15m),另三边用40m长的木栏围成.
如图,某农场建一个矩形的养鸡场,鸡场的一边靠墙(墙长15m),另三边用40m长的木栏围成.