题目内容
在正方形ABCD中,点P是CD边上一动点,连接PA,分别过点B、D作BE⊥PA、DF⊥PA,垂足分别为E、F.
(1)如图①,请探究BE、DF、EF这三条线段的长度具有怎样的数量关系?
(2)若点P在DC的延长线上,如图②,那么这三条线段的长度之间又具有怎样的数量关系?
(3)若点P在CD的延长线上,如图③,请直接写出结论.

(1)如图①,请探究BE、DF、EF这三条线段的长度具有怎样的数量关系?
(2)若点P在DC的延长线上,如图②,那么这三条线段的长度之间又具有怎样的数量关系?
(3)若点P在CD的延长线上,如图③,请直接写出结论.

考点:全等三角形的判定与性质,正方形的性质
专题:计算题
分析:(1)在图①中BE、DF、EF这三条线段长度具有这样的数量关系:BE-DF=EF,理由为:由BE垂直于AP,DF垂直于AP,得到一对直角相等,再由四边形ABCD为正方形,得到AB=AD,且∠BAD为直角,利用同角的余角相等得到一对角相等,利用AAS得到三角形ABE与三角形DFA全等,利用全等三角形对应边相等得到BE=AF,AE=DF,根据AF-AE=EF,等量代换即可得证;
(2)在图②中BE、DF、EF这三条线段长度具有这样的数量关系:DF-BE=EF,理由同(1);
(3)在图③中BE、DF、EF这三条线段长度具有这样的数量关系:DF+BE=EF,理由同(1).
(2)在图②中BE、DF、EF这三条线段长度具有这样的数量关系:DF-BE=EF,理由同(1);
(3)在图③中BE、DF、EF这三条线段长度具有这样的数量关系:DF+BE=EF,理由同(1).
解答:解:(1)在图①中BE、DF、EF这三条线段长度具有这样的数量关系:BE-DF=EF;
证明:∵BE⊥PA,DF⊥PA,
∴∠BEA=∠AFD=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAE+∠DAF=90°,
又∵∠AFD=90°,
∴∠ADF+∠DAF=90°,
∴∠BAE=∠ADF,
在△BAE和△ADF中,
∴△BAE≌△ADF(AAS),
∴BE=AF,AE=DF,
∵AE-AF=EF,
∴DF-BE=EF.
(2)在图②中BE、DF、EF这三条线段长度具有这样的数量关系:DF-BE=EF;
∵BE⊥PA,DF⊥PA,
∴∠BEA=∠AFD=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAE+∠DAF=90°,
又∵∠AFD=90°,
∴∠ADF+∠DAF=90°,
∴∠BAE=∠ADF,
在△BAE和△ADF中,
∴△BAE≌△ADF(AAS),
∴BE=AF,AE=DF,
∵AE-AF=EF,
∴DF-BE=EF.
(3)在图③中BE、DF、EF这三条线段长度具有这样的数量关系:DF+BE=EF,
理由为:∵BE⊥PA,DF⊥PA,
∴∠BEA=∠AFD=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAE+∠DAF=90°,
又∵∠AFD=90°,
∴∠ADF+∠DAF=90°,
∴∠BAE=∠ADF,
在△BAE和△ADF中,
∴△BAE≌△ADF(AAS),
∴BE=AF,AE=DF,
∵AE+AF=EF,
∴DF+BE=EF.
证明:∵BE⊥PA,DF⊥PA,
∴∠BEA=∠AFD=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAE+∠DAF=90°,
又∵∠AFD=90°,
∴∠ADF+∠DAF=90°,
∴∠BAE=∠ADF,
在△BAE和△ADF中,
|
∴△BAE≌△ADF(AAS),
∴BE=AF,AE=DF,
∵AE-AF=EF,
∴DF-BE=EF.
(2)在图②中BE、DF、EF这三条线段长度具有这样的数量关系:DF-BE=EF;
∵BE⊥PA,DF⊥PA,
∴∠BEA=∠AFD=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAE+∠DAF=90°,
又∵∠AFD=90°,
∴∠ADF+∠DAF=90°,
∴∠BAE=∠ADF,
在△BAE和△ADF中,
|
∴△BAE≌△ADF(AAS),
∴BE=AF,AE=DF,
∵AE-AF=EF,
∴DF-BE=EF.
(3)在图③中BE、DF、EF这三条线段长度具有这样的数量关系:DF+BE=EF,
理由为:∵BE⊥PA,DF⊥PA,
∴∠BEA=∠AFD=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAE+∠DAF=90°,
又∵∠AFD=90°,
∴∠ADF+∠DAF=90°,
∴∠BAE=∠ADF,
在△BAE和△ADF中,
|
∴△BAE≌△ADF(AAS),
∴BE=AF,AE=DF,
∵AE+AF=EF,
∴DF+BE=EF.
点评:此题考查了全等三角形的判定与性质,正方形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
 如图,矩形ABCD中,点G是AD的中点,GE⊥CG交AB于E,BE=BC,连CE交BG于F,则∠BFC等于( )
如图,矩形ABCD中,点G是AD的中点,GE⊥CG交AB于E,BE=BC,连CE交BG于F,则∠BFC等于( )| A、45° | B、60° |
| C、67.5° | D、72° |
已知2x-3y=1,用含x的代数式表示y正确的是( )
A、y=
| ||||
B、x=
| ||||
C、y=
| ||||
D、y=-
|
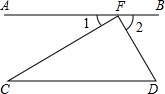 完成下面证明,并在下面括号里,填上推理的根据.
完成下面证明,并在下面括号里,填上推理的根据. 如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度. 如图,在?ABCD中,E、F分别是AB,CD的中点,求证:DE=BF.
如图,在?ABCD中,E、F分别是AB,CD的中点,求证:DE=BF. 小刚家的住房结构如图(单位:米),小刚的爸爸打算把卧室、卫生间、厨房和客厅都铺上地砖,请你帮他算一算,至少需要买多少平方米的地砖?
小刚家的住房结构如图(单位:米),小刚的爸爸打算把卧室、卫生间、厨房和客厅都铺上地砖,请你帮他算一算,至少需要买多少平方米的地砖?