题目内容
14.经过A(4,0),B(-2,0),C(0,3)三点的抛物线解析式是y=-$\frac{3}{8}$x2+$\frac{3}{4}$x+3.分析 根据A与B坐标特点设出抛物线解析式为y=a(x-2)(x-4),把C坐标代入求出a的值,即可确定出解析式.
解答 解:根据题意设抛物线解析式为y=a(x+2)(x-4),
把C(0,3)代入得:-8a=3,即a=-$\frac{3}{8}$,
则抛物线解析式为y=-$\frac{3}{8}$(x+2)(x-4)=-$\frac{3}{8}$x2+$\frac{3}{4}$x+3,
故答案为y=-$\frac{3}{8}$x2+$\frac{3}{4}$x+3.
点评 此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
5.化简:$\frac{x}{x-y}$-$\frac{y}{x+y}$,结果正确的是( )
| A. | 1 | B. | $\frac{{x}^{2}+{y}^{2}}{{x}^{2}-{y}^{2}}$ | C. | $\frac{x-y}{x+y}$ | D. | x2+y2 |
2. 某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取10%进行调查,根据调查结果绘制了如图不完整的频数分布表和扇形统计图:
某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取10%进行调查,根据调查结果绘制了如图不完整的频数分布表和扇形统计图:
请根据以上图表信息解答下列问题:
(1)频数分布表中的a=24,b=18;
(2)在扇形统计图中,“排球”所在的扇形的圆心角为54度;
(3)全校有多少名学生选择参加乒乓球运动?
 某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取10%进行调查,根据调查结果绘制了如图不完整的频数分布表和扇形统计图:
某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取10%进行调查,根据调查结果绘制了如图不完整的频数分布表和扇形统计图:| 运动项目 | 频数(人数) |
| 羽毛球 | 30 |
| 篮球 | a |
| 乒乓球 | 36 |
| 排球 | b |
| 足球 | 12 |
(1)频数分布表中的a=24,b=18;
(2)在扇形统计图中,“排球”所在的扇形的圆心角为54度;
(3)全校有多少名学生选择参加乒乓球运动?
9.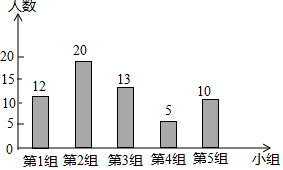 九年级(2)班同学根据兴趣分成五个小组,各小组人数分布如图所示,则在扇形图中,第一小组对应的圆心角度数是( )
九年级(2)班同学根据兴趣分成五个小组,各小组人数分布如图所示,则在扇形图中,第一小组对应的圆心角度数是( )
 九年级(2)班同学根据兴趣分成五个小组,各小组人数分布如图所示,则在扇形图中,第一小组对应的圆心角度数是( )
九年级(2)班同学根据兴趣分成五个小组,各小组人数分布如图所示,则在扇形图中,第一小组对应的圆心角度数是( )| A. | 45° | B. | 60° | C. | 72° | D. | 120° |
19.对于函数y=2x-1,下列说法正确的是( )
| A. | 它的图象过点(1,0) | B. | y值随着x值增大而减小 | ||
| C. | 它的图象经过第二象限 | D. | 当x>1时,y>0 |
18. 如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D'、C'的位置.若∠CFC′=150°,则∠AED′等于( )
如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D'、C'的位置.若∠CFC′=150°,则∠AED′等于( )
 如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D'、C'的位置.若∠CFC′=150°,则∠AED′等于( )
如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D'、C'的位置.若∠CFC′=150°,则∠AED′等于( )| A. | 50° | B. | 45° | C. | 40° | D. | 30° |
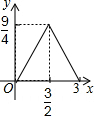
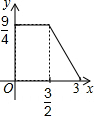
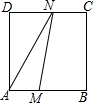 如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自D点出发沿折线DC-CB以每秒2cm的速度运动,到达B点时运动同时停止,设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是( )
如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自D点出发沿折线DC-CB以每秒2cm的速度运动,到达B点时运动同时停止,设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是( )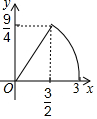
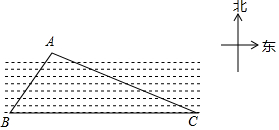 如图,已知一条东西走向的河流,在河流对岸有一点A,小明在岸边点B处测得点A在点B的北偏东30°方向上,小明沿河岸向东走80m后到达点C,测得点A在点C的北偏西60°方向上,则点A到河岸BC的距离为20$\sqrt{3}$米.
如图,已知一条东西走向的河流,在河流对岸有一点A,小明在岸边点B处测得点A在点B的北偏东30°方向上,小明沿河岸向东走80m后到达点C,测得点A在点C的北偏西60°方向上,则点A到河岸BC的距离为20$\sqrt{3}$米.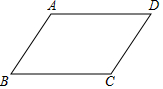 已知平行四边形ABCD.
已知平行四边形ABCD.