题目内容
13．不等式组$\left\{\begin{array}{l}x-1≤0\\ 2x-5＜1\end{array}\right.$的解集为（ ）| A． | x＜-2 | B． | x≤-1 | C． | x≤1 | D． | x＜3 |
分析 先求出每个不等式的解集，再求出每个解集的公共部分即可．
解答 解：$\left\{\begin{array}{l}{x-1≤0①}\\{2x-5＜1②}\end{array}\right.$
解不等式①得：x≤1，
解不等式②得：x＜3，
∴不等式组的解集为x≤1，
故选C．
点评 本题考查了解一元一次不等式组的应用，能根据不等式的解集找出不等式组的解集是解此题的关键．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
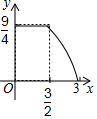
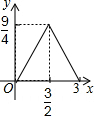
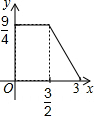
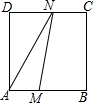如图，在正方形ABCD中，AB=3cm，动点M自A点出发沿AB方向以每秒1cm的速度运动，同时动点N自D点出发沿折线DC-CB以每秒2cm的速度运动，到达B点时运动同时停止，设△AMN的面积为y（cm2），运动时间为x（秒），则下列图象中能大致反映y与x之间函数关系的是（ ）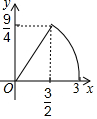
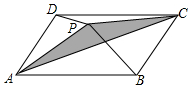如上右图，已知P是平行四边形ABCD内一点，且S△PAB=7，S△PAD=4，则阴影部分的面积是3．
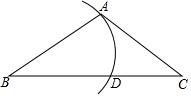如图，则△ABC中，∠BAC=100°，AB=AC=4，以点B为圆心，BA长为半径作圆弧，交BC于点D，则$\widehat{AD}$的长为$\frac{8π}{9}$．（结果保留π）
5．化简：$\frac{x}{x-y}$-$\frac{y}{x+y}$，结果正确的是（ ）
| A． | 1 | B． | $\frac{{x}^{2}+{y}^{2}}{{x}^{2}-{y}^{2}}$ | C． | $\frac{x-y}{x+y}$ | D． | x2+y2 |
2．
某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动，每位同学必须且只能选择一项球类运动，对该校学生随机抽取10%进行调查，根据调查结果绘制了如图不完整的频数分布表和扇形统计图：
请根据以上图表信息解答下列问题：
（1）频数分布表中的a=24，b=18；
（2）在扇形统计图中，“排球”所在的扇形的圆心角为54度；
（3）全校有多少名学生选择参加乒乓球运动？
某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动，每位同学必须且只能选择一项球类运动，对该校学生随机抽取10%进行调查，根据调查结果绘制了如图不完整的频数分布表和扇形统计图：| 运动项目 | 频数（人数） |
| 羽毛球 | 30 |
| 篮球 | a |
| 乒乓球 | 36 |
| 排球 | b |
| 足球 | 12 |
（1）频数分布表中的a=24，b=18；
（2）在扇形统计图中，“排球”所在的扇形的圆心角为54度；
（3）全校有多少名学生选择参加乒乓球运动？
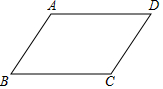已知平行四边形ABCD．