题目内容
4.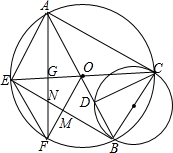 如图,已知四边形AEBC,对角线AB,CE为⊙O的直径,以BC为直径的圆与AB交与点D,连接CD,过点O作OF⊥BE于点M,OF交⊙O于点F,连接AF,交CB于点G,交BE于点N,连接EF.若∠BCD=30°.
如图,已知四边形AEBC,对角线AB,CE为⊙O的直径,以BC为直径的圆与AB交与点D,连接CD,过点O作OF⊥BE于点M,OF交⊙O于点F,连接AF,交CB于点G,交BE于点N,连接EF.若∠BCD=30°.(1)四边形AEBC是矩形;
(2)求证:△AEG≌△CBD;
(3)△EFN与△ACO是否相似?若相似,请求出相似比;若不相似,请说明理由.
分析 (1)运用直径所对的圆周角是90°,即可求解;
(2)根据同弧(等弧)所对的圆周角相等,和垂径定理得出∠3=∠BCD=30°,∠2=∠1=60,由矩形性质得出AE=BC,即可证明全等;
(3)由(2)中结论,结合直径所对的圆周角为90°,可以得出:∠5=∠6=∠7=∠8=30°,即可证明相似;
解答 解:(1)∵AB,CE为⊙O的直径,
∴∠CAE=∠ACB=∠CBE=90°,
∴四边形AEBC是矩形;
(2)如图1,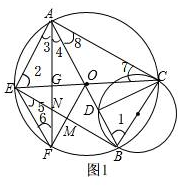
由(1)知,四边形AEBC是矩形,
∴AE=BC,
∵以BC为直径的圆与AB交与点D,
∴∠BDC=90°,
由∠BCD=90°,可求:∠1=60°,
∴∠2=∠1=60°,
∵OA=OE,
∴△OAE为等边三角形,
∴∠OAE=60°,
∵OF⊥BE,
∴弧EF=弧BF,
∴∠3=∠4=30°,
∴∠3=∠BCD,
在△AEG和CBD中,
$\left\{\begin{array}{l}{∠2=∠1}\\{AE=BC}\\{∠3=∠BCD}\end{array}\right.$,
∴△AEG≌△CBD;
(3)如图2
∵AB,CE为⊙O的直径,
∴∠CAE=∠ACB=∠CBE=90°,
由(2)知∠2=∠1=60°,
可求:∠7=∠8=30°,
∴∠6=∠7=30°,
由(2)知,弧EF=弧BF,∠4=30°,
∴∠5=∠4=30°,
∴∠5=∠6=∠7=∠8=30°,
∴△EFN∽△ACO;
∴∠3=∠6=30°,
∴EF=AE,
在Rt△AEC中,∠7=30°,
∴$\frac{AE}{AC}$=tan∠7=tan30°=$\frac{\sqrt{3}}{3}$;
∴两三角形的相似比为:$\frac{\sqrt{3}}{3}$.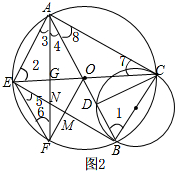
点评 此题主要考查圆的综合问题,熟悉圆的相关性质,会进行三角形全等和相似的证明,熟悉矩形的判定方法,会适当运用三角函数是解题的关键.

| A. |  | B. |  | C. |  | D. |  |
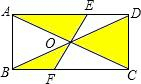 如图,矩形ABCD中,对角线AC、BD交于点O,过O的直线分别交AD、BC于点E、F,已知AD=4cm,图中阴影部分的面积总和为6cm2,对角线AC长为( )
如图,矩形ABCD中,对角线AC、BD交于点O,过O的直线分别交AD、BC于点E、F,已知AD=4cm,图中阴影部分的面积总和为6cm2,对角线AC长为( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
| A. | A校多于B校 | B. | A校与B校一样多 | C. | A校少于B校 | D. | 不能确定 |
 如图所示,直线AB,CD被直线MN所截,分别交于M,N两点,且AB∥CD,∠1=75°,求∠2的度数.
如图所示,直线AB,CD被直线MN所截,分别交于M,N两点,且AB∥CD,∠1=75°,求∠2的度数.