题目内容
13.PA、PB分别是⊙O的切线,切点分别为A、B,∠AOB=144°,则∠P=36°.分析 根据切线的性质得出∠PAO=∠PBO=90°,根据四边形的内角和定理求出即可.
解答 解:如图所示:
∵PA、PB是⊙O的切线,A、B是切点,
∴∠PAO=∠PBO=90°,
∵∠AOB=144°,
∴∠APB=360°-90°-90°-144°=36°,
故答案为:36°.
点评 本题考查了圆的切线的性质,由定理可知,若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
5.估计$\sqrt{10}$的值在哪两个整数之间( )
| A. | 9和10 | B. | 7和8 | C. | 5和6 | D. | 3和4 |
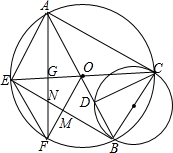 如图,已知四边形AEBC,对角线AB,CE为⊙O的直径,以BC为直径的圆与AB交与点D,连接CD,过点O作OF⊥BE于点M,OF交⊙O于点F,连接AF,交CB于点G,交BE于点N,连接EF.若∠BCD=30°.
如图,已知四边形AEBC,对角线AB,CE为⊙O的直径,以BC为直径的圆与AB交与点D,连接CD,过点O作OF⊥BE于点M,OF交⊙O于点F,连接AF,交CB于点G,交BE于点N,连接EF.若∠BCD=30°.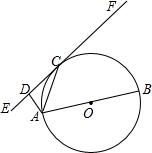 如图,AB是⊙O直径,EF切⊙O于C,AD⊥EF于D,求证:AC2=AD•AB.
如图,AB是⊙O直径,EF切⊙O于C,AD⊥EF于D,求证:AC2=AD•AB.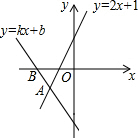 如图,直线y=kx+b与直线y=2x+1相交于点A(-1,-1),则不等式kx+b<2x+1<0的解集为x<-1-1<x<-$\frac{1}{2}$.
如图,直线y=kx+b与直线y=2x+1相交于点A(-1,-1),则不等式kx+b<2x+1<0的解集为x<-1-1<x<-$\frac{1}{2}$.