题目内容
7.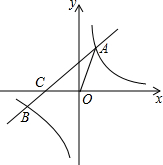 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于第一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,3),点B的坐标为(-6,n).
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于第一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,3),点B的坐标为(-6,n).(1)求该反比例函数和一次函数的解析式;
(2)在x轴上取一点D,使得△AOD的面积等于△AOC的面积的2倍,求出D点的坐标.
分析 (1)根据待定系数法就可以求出函数的解析式;
(2)根据直线求得C的坐标,然后设D(x,0),根据△AOD的面积等于△AOC的面积的2倍,得出关于x的方程,解方程即可求得.
解答 解:(1)∵点A(2,3)在反比例函数图象上
∴m=2×3=6
即反比例函数关系式为y=$\frac{6}{x}$,
∵点B(-6,n)在反比例函数图象上
∴n=-1,
∵点A(2,3)和B(-6,-1)在一次函数y=kx+b的图象上
∴$\left\{\begin{array}{l}{2k+b=3}\\{-6k+b=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴一次函数关系式为y=$\frac{1}{2}$x+2;
(2)由直线y=$\frac{1}{2}$x+2可知C(-4,0),
∵A(2,3),
∴S△AOC=$\frac{1}{2}$×4×3=6,
∵△AOD的面积等于△AOC的面积的2倍,
∴S△AOD=12,
设D(x,0),
则S△AOD=$\frac{1}{2}$|x|×3=12,
∴x=±8,
∴D(-8,0)或(8,0).
点评 本题考查了反比例函数与一次函数的交点问题,待定系数法求函数解析式以及三角形的面积,熟练掌握待定系数法是解题的关键.

练习册系列答案
相关题目
18.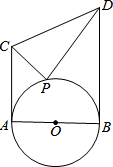 如图,⊙O的半径为1,AC⊥AB于A,BD⊥AB于B,AC=2,BD=3,P为半圆上一点,则△PCD面积的最小值是( )
如图,⊙O的半径为1,AC⊥AB于A,BD⊥AB于B,AC=2,BD=3,P为半圆上一点,则△PCD面积的最小值是( )
 如图,⊙O的半径为1,AC⊥AB于A,BD⊥AB于B,AC=2,BD=3,P为半圆上一点,则△PCD面积的最小值是( )
如图,⊙O的半径为1,AC⊥AB于A,BD⊥AB于B,AC=2,BD=3,P为半圆上一点,则△PCD面积的最小值是( )| A. | $\frac{3}{2}$ | B. | $\frac{9}{5}$ | C. | $\frac{{\sqrt{5}}}{4}$ | D. | $\frac{{5-\sqrt{5}}}{2}$ |
2. 如图所示的几何体是由5个相同的小正方体组成,其主视图为( )
如图所示的几何体是由5个相同的小正方体组成,其主视图为( )
 如图所示的几何体是由5个相同的小正方体组成,其主视图为( )
如图所示的几何体是由5个相同的小正方体组成,其主视图为( )| A. |  | B. |  | C. |  | D. |  |
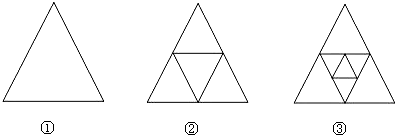
12. 张萌取三个如图所示的面积为4cm2的钝角三角形按如图所示的方式相连接,拼成了一个正六边形,则拼成的正六边形的面积为( )
张萌取三个如图所示的面积为4cm2的钝角三角形按如图所示的方式相连接,拼成了一个正六边形,则拼成的正六边形的面积为( )
 张萌取三个如图所示的面积为4cm2的钝角三角形按如图所示的方式相连接,拼成了一个正六边形,则拼成的正六边形的面积为( )
张萌取三个如图所示的面积为4cm2的钝角三角形按如图所示的方式相连接,拼成了一个正六边形,则拼成的正六边形的面积为( )| A. | 12cm2 | B. | 20cm2 | C. | 24cm2 | D. | 32cm2 |
19. 某商品的外包装盒的三视图如图所示,则这个包装盒的侧面积为( )
某商品的外包装盒的三视图如图所示,则这个包装盒的侧面积为( )
 某商品的外包装盒的三视图如图所示,则这个包装盒的侧面积为( )
某商品的外包装盒的三视图如图所示,则这个包装盒的侧面积为( )| A. | 150πcm2 | B. | 200πcm2 | C. | 300πcm2 | D. | 400πcm2 |
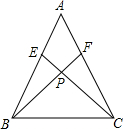 在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:△EBC≌△FCB.
在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:△EBC≌△FCB.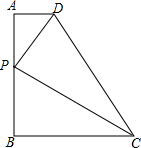 如图,已知直角梯形ABCD,∠A=∠B=90°,AD=2,BC=8,AB=10,在线段AB上取一点P,使△ADP与△BCP相似,求AP的长.
如图,已知直角梯形ABCD,∠A=∠B=90°,AD=2,BC=8,AB=10,在线段AB上取一点P,使△ADP与△BCP相似,求AP的长.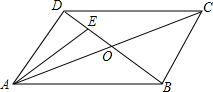 如图,在?ABCD中,对角线AC,BD相交于点O,AC=2AD,点E是OD的中点,连接AE.
如图,在?ABCD中,对角线AC,BD相交于点O,AC=2AD,点E是OD的中点,连接AE.