题目内容
15.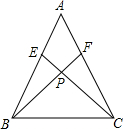 在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:△EBC≌△FCB.
在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:△EBC≌△FCB.
分析 首先根据等边对等角可得∠ABC=∠ACB,再根据等式的性质可得BE=CF,然后再利用SAS判定△EBC≌△FCB.
解答 证明:∵AB=AC,
∴∠ABC=∠ACB,
∵AE=AF,
∴AB-AE=AC-AF
即BE=CF,
在△EBC和△FCB中,$\left\{\begin{array}{l}{EB=CF}\\{∠ABC=∠ACB}\\{BC=BC}\end{array}\right.$,
∴△EBC≌△FCB(SAS).
点评 本题考查三角形全等的判定方法,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
相关题目
6.下列图案中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10. 如图,在△ABC中,分别以顶点A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线MN,与AB交于点O,以O为圆心,OA为半径作圆,⊙O恰好经过点C.下列结论中,错误的是( )
如图,在△ABC中,分别以顶点A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线MN,与AB交于点O,以O为圆心,OA为半径作圆,⊙O恰好经过点C.下列结论中,错误的是( )
 如图,在△ABC中,分别以顶点A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线MN,与AB交于点O,以O为圆心,OA为半径作圆,⊙O恰好经过点C.下列结论中,错误的是( )
如图,在△ABC中,分别以顶点A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线MN,与AB交于点O,以O为圆心,OA为半径作圆,⊙O恰好经过点C.下列结论中,错误的是( )| A. | AB是⊙O的直径 | B. | ∠ACB=90° | ||
| C. | △ABC是⊙O内接三角形 | D. | O是△ABC的内心 |
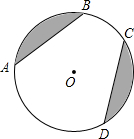 如图,$\widehat{AB}$+$\widehat{CD}$=$\widehat{AD}$+$\widehat{BC}$,弦AB长为8,DC长为4,则S阴影为10π-16.
如图,$\widehat{AB}$+$\widehat{CD}$=$\widehat{AD}$+$\widehat{BC}$,弦AB长为8,DC长为4,则S阴影为10π-16.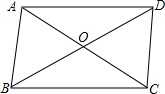 如图,在?ABCD中,对角线AC、BD相交成的锐角为60°,若AC=6,BD=8,求?ABCD的面积.($\sqrt{3}≈1.73$,结果精确到0.1)
如图,在?ABCD中,对角线AC、BD相交成的锐角为60°,若AC=6,BD=8,求?ABCD的面积.($\sqrt{3}≈1.73$,结果精确到0.1)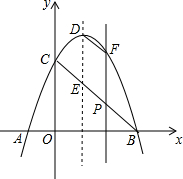 如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,线段BC与抛物线的对称轴交于点E、P为线段BC上的一点(不与点B、C重合),过点P作PF∥y轴交抛物线于点F,连结DF.设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,线段BC与抛物线的对称轴交于点E、P为线段BC上的一点(不与点B、C重合),过点P作PF∥y轴交抛物线于点F,连结DF.设点P的横坐标为m.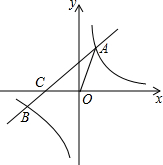 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于第一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,3),点B的坐标为(-6,n).
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于第一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,3),点B的坐标为(-6,n).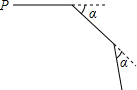 如图,鹏鹏从点P出发,沿直线前进10米后向右转α,接着沿直线前进10米,再向右转α,…,照这样走下去,他第一次回到出发地点P时,一共走了100米,则α的度数为36°.
如图,鹏鹏从点P出发,沿直线前进10米后向右转α,接着沿直线前进10米,再向右转α,…,照这样走下去,他第一次回到出发地点P时,一共走了100米,则α的度数为36°.