题目内容
16.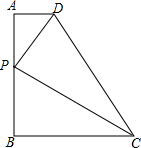 如图,已知直角梯形ABCD,∠A=∠B=90°,AD=2,BC=8,AB=10,在线段AB上取一点P,使△ADP与△BCP相似,求AP的长.
如图,已知直角梯形ABCD,∠A=∠B=90°,AD=2,BC=8,AB=10,在线段AB上取一点P,使△ADP与△BCP相似,求AP的长.
分析 首先设AP=x,则BP=AB-AP=10-x,然后分别从当$\frac{PA}{PB}=\frac{AD}{BC}$时,△APD∽△BPC与当$\frac{PA}{BC}=\frac{AD}{BP}$时,△APD∽△BCP;去分析求解即可求得答案.
解答 解:设AP=x,则BP=AB-AP=10-x,
∵直角梯形ABCD,∠A=∠B=90°,
∴①当$\frac{PA}{PB}=\frac{AD}{BC}$时,△APD∽△BPC,
即$\frac{x}{10-x}=\frac{2}{8}$,
解得:x=2;
②当$\frac{PA}{BC}=\frac{AD}{BP}$时,△APD∽△BCP,
即$\frac{x}{8}=\frac{2}{10-x}$,
解得:x=2或x=8;
综上所述:AP=2或8.
点评 此题考查了相似三角形的判定与性质.注意掌握分类讨论思想的应用是解此题的关键.

练习册系列答案
相关题目
6.下列图案中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
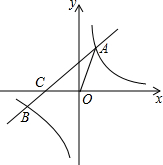 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于第一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,3),点B的坐标为(-6,n).
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于第一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,3),点B的坐标为(-6,n).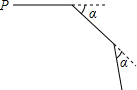 如图,鹏鹏从点P出发,沿直线前进10米后向右转α,接着沿直线前进10米,再向右转α,…,照这样走下去,他第一次回到出发地点P时,一共走了100米,则α的度数为36°.
如图,鹏鹏从点P出发,沿直线前进10米后向右转α,接着沿直线前进10米,再向右转α,…,照这样走下去,他第一次回到出发地点P时,一共走了100米,则α的度数为36°.



 如图,两平面镜l,m的夹角为α,入射光线A0平行于m入射到l上,经过两次反射后射出的反射光线O′B与l平行,则∠α=60°.
如图,两平面镜l,m的夹角为α,入射光线A0平行于m入射到l上,经过两次反射后射出的反射光线O′B与l平行,则∠α=60°. 已知:m、n是方程x2-6x+5=0的两个实数根,且m<n,抛物线y=-x2+bx+c的图象经过点A(-m,0)、B(0,n).
已知:m、n是方程x2-6x+5=0的两个实数根,且m<n,抛物线y=-x2+bx+c的图象经过点A(-m,0)、B(0,n).