题目内容
12. 张萌取三个如图所示的面积为4cm2的钝角三角形按如图所示的方式相连接,拼成了一个正六边形,则拼成的正六边形的面积为( )
张萌取三个如图所示的面积为4cm2的钝角三角形按如图所示的方式相连接,拼成了一个正六边形,则拼成的正六边形的面积为( )| A. | 12cm2 | B. | 20cm2 | C. | 24cm2 | D. | 32cm2 |
分析 根据题意得出面积为4cm2的钝角三角形为等腰三角形,顶角∠BAC=120°,∠B=∠C=30°,△DBC为等边三角形,作AM⊥BC于M,设AM=x,则AB=2x,BM=$\sqrt{3}$x,BC=2$\sqrt{3}$x,由三角形的面积得出$\sqrt{3}$x2=4,连接DM,则DM⊥BC,由等边三角形的性质得出DM=$\sqrt{3}$BM=3x,求出△BCD的面积,即可得出结果.
解答 解:如图所示: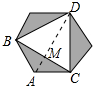
根据题意得:面积为4cm2的钝角三角形为等腰三角形,顶角∠BAC=120°,∠B=∠C=30°,△DBC为等边三角形,
作AM⊥BC于M,
设AM=x,则AB=2x,BM=$\sqrt{3}$x,
∴BC=2$\sqrt{3}$x,
∴$\frac{1}{2}$•2$\sqrt{3}$x•x=4,
∴$\sqrt{3}$x2=4,
连接DM,则DM⊥BC,
∴DM$\sqrt{3}$BM=3x,
∴△BCD的面积=$\frac{1}{2}$BC•DM=$\frac{1}{2}$×2$\sqrt{3}$x•3x=3$\sqrt{3}$x2=3×4=12,
∴拼成的正六边形的面积=3×4+12=24(cm2);
故选:C.
点评 本题考查了正多边形和圆、等腰三角形的性质、等边三角形的性质、三角形面积的计算等知识;通过设未知数求出△BCD的面积是解决问题的突破口.

练习册系列答案
相关题目
2.下列说法不正确的是( )
| A. | 对顶角相等 | |
| B. | 过任意一点可作已知直线的一条平行线 | |
| C. | 两点之间线段最短 | |
| D. | 同一平面内,过一点有且只有一条直线与已知直线垂直 |
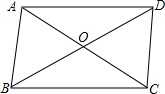 如图,在?ABCD中,对角线AC、BD相交成的锐角为60°,若AC=6,BD=8,求?ABCD的面积.($\sqrt{3}≈1.73$,结果精确到0.1)
如图,在?ABCD中,对角线AC、BD相交成的锐角为60°,若AC=6,BD=8,求?ABCD的面积.($\sqrt{3}≈1.73$,结果精确到0.1)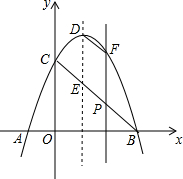 如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,线段BC与抛物线的对称轴交于点E、P为线段BC上的一点(不与点B、C重合),过点P作PF∥y轴交抛物线于点F,连结DF.设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,线段BC与抛物线的对称轴交于点E、P为线段BC上的一点(不与点B、C重合),过点P作PF∥y轴交抛物线于点F,连结DF.设点P的横坐标为m.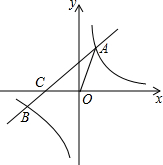 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于第一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,3),点B的坐标为(-6,n).
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于第一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,3),点B的坐标为(-6,n).

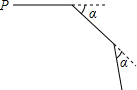 如图,鹏鹏从点P出发,沿直线前进10米后向右转α,接着沿直线前进10米,再向右转α,…,照这样走下去,他第一次回到出发地点P时,一共走了100米,则α的度数为36°.
如图,鹏鹏从点P出发,沿直线前进10米后向右转α,接着沿直线前进10米,再向右转α,…,照这样走下去,他第一次回到出发地点P时,一共走了100米,则α的度数为36°. 如图,两平面镜l,m的夹角为α,入射光线A0平行于m入射到l上,经过两次反射后射出的反射光线O′B与l平行,则∠α=60°.
如图,两平面镜l,m的夹角为α,入射光线A0平行于m入射到l上,经过两次反射后射出的反射光线O′B与l平行,则∠α=60°.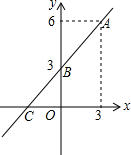 如图,一次函数y=kx+b的图象经过A,B两点,求一次函数的解析式及△AOC的面积.
如图,一次函数y=kx+b的图象经过A,B两点,求一次函数的解析式及△AOC的面积.