题目内容
17.图①是一个三角形,分别连接这个三角形三边的中点得到图②,再分别连接图②中间小三角形三边的中点,得到图③.(1)图②有5个三角形;图③有9个三角形.
(2)按上面的方法继续下去,第n个图形中有多少个三角形?(用n的代数式表示结论)
(3)有没有一个图形中存在2016个三角形?如果存在,请求出是第几个三角形;如果不存在,请说明理由.
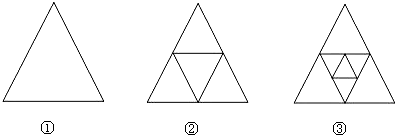
分析 (1)根据图形的变化可发现每个图形比前一个图形多4个三角形,结合图①有一个三角形即可得出结论;(2)根据图形的变化可发现每个图形比前一个图形多4个三角形,而图形①只有一个三角形,用含n的代数式表示出结论即可;(3)结合(2)的结论,令三角形的个数等于2016,看n的值是否为整数,是的话则第n个图形就是所求,如果不是,则不存在.
解答 解:根据图形的变化可知每个图形比前一个图形多4个三角形.
(1)由发现的规律可知图②有1+4=5个三角形;图③有5+4=9个三角形.
故答案为:5;9.
(2)4×(n-1)+1=4n-3.
故按上面的方法继续下去,第n个图形中有4n-3个三角形.
(3)令4n-3=2016,解得n=504…3,
∵商出现了余数,即得数不是整数,
∴没有一个图形中存在2016个三角形.
点评 本题考查了图形变化类中的三角形的变化,解题的关键是:根据图形的变化发现每个图形比前一个图形多4个三角形.本题属于基础题,难度不大,只要按照后面图形的画法,分析图②图③即可得出结论,唯一的失分点是忘记结合图①一个三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.我省2014年的快递业务量为1.8亿件,受益于电子商务发展和法治环境改善等多冲因素,快递业务迅猛发展,2015年增速位居全国第一.若2016年的快递业务量达到5亿件,设2014年与2015年这两年的平均增长率为x,则下列方程正确的是( )
| A. | 1.8(1+x)=5 | B. | 1.8(1+2x)=5 | ||
| C. | 1.8(1+x)2=5 | D. | 1.8(1+x)+1.8(1+x)2=5 |
2.下列说法不正确的是( )
| A. | 对顶角相等 | |
| B. | 过任意一点可作已知直线的一条平行线 | |
| C. | 两点之间线段最短 | |
| D. | 同一平面内,过一点有且只有一条直线与已知直线垂直 |
9.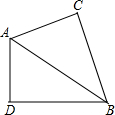 如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )
如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )
 如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )
如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )| A. | SSS | B. | SAS | C. | HL | D. | AAS |
6.下列图案中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
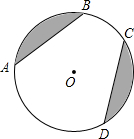 如图,$\widehat{AB}$+$\widehat{CD}$=$\widehat{AD}$+$\widehat{BC}$,弦AB长为8,DC长为4,则S阴影为10π-16.
如图,$\widehat{AB}$+$\widehat{CD}$=$\widehat{AD}$+$\widehat{BC}$,弦AB长为8,DC长为4,则S阴影为10π-16. 平移△ABC,使点A移动到点A′,画出平移后的△A′B′C′.
平移△ABC,使点A移动到点A′,画出平移后的△A′B′C′.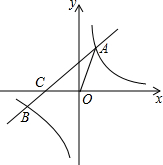 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于第一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,3),点B的坐标为(-6,n).
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于第一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,3),点B的坐标为(-6,n).