题目内容
长为l的一根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边x的取值范围为__________.
 ≤x<
【解析】试题解析:∵围成两个全等的三角形可得两个三角形的周长相等,
∴可得
又因为x为最长边大于周长的,
综上可得
故答案为:
≤x<
【解析】试题解析:∵围成两个全等的三角形可得两个三角形的周长相等,
∴可得
又因为x为最长边大于周长的,
综上可得
故答案为:
 阅读快车系列答案
阅读快车系列答案下列命题中的真命题是( )
A. 锐角大于它的余角 B. 锐角大于它的补角
C. 钝角大于它的补角 D. 锐角与钝角之和等于平角
 C
【解析】试题分析:A、锐角大于它的余角,不一定成立,故本选项错误;
B、锐角小于它的补角,故本选项错误;
C、钝角大于它的补角,本选项正确;
D、锐角与钝角之和等于平角,不一定成立,故本选项错误.
故选:C.
C
【解析】试题分析:A、锐角大于它的余角,不一定成立,故本选项错误;
B、锐角小于它的补角,故本选项错误;
C、钝角大于它的补角,本选项正确;
D、锐角与钝角之和等于平角,不一定成立,故本选项错误.
故选:C. 有一个小正方体,正方体的每个面分别标有1,2,3,4,5,6这六个数字.现在有甲、乙两位同学做游戏,游戏规则是:任意掷出正方体后,如果朝上的数字是6,甲是胜利者;如果朝上的数字不是6,乙是胜利者.你认为这个游戏规则对甲、乙双方公平吗?为什么?如果不公平,你打算怎样修改才能使游戏规则对甲、乙双方公平?
 (1)这个游戏不公平.(2)游戏规则修改见解析(答案不唯一)
【解析】试题分析:分别求出甲胜利的概率和乙胜利的概率,比较大小看判断游戏是否公平,游戏规则修改只要是两人获胜的概率相等即可.
试题解析:(1)这个游戏不公平.因为正方体的每个面分别标有1,2,3,4,5,6这六个数字,其中数字6只有1个,也就是甲胜利的概率是;不是6的数字有5个,也就是说乙胜利的概率是,双方的胜利的机会不是均...
(1)这个游戏不公平.(2)游戏规则修改见解析(答案不唯一)
【解析】试题分析:分别求出甲胜利的概率和乙胜利的概率,比较大小看判断游戏是否公平,游戏规则修改只要是两人获胜的概率相等即可.
试题解析:(1)这个游戏不公平.因为正方体的每个面分别标有1,2,3,4,5,6这六个数字,其中数字6只有1个,也就是甲胜利的概率是;不是6的数字有5个,也就是说乙胜利的概率是,双方的胜利的机会不是均... 某校九年级(1)班50名学生中有20名团员,他们都积极报名参加学校开展的“文明劝导活动”。根据要求,该班从团员中随机抽取1名参加,则该班团员京京被抽到的概率是 【 】
A.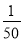 B.
B.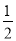 C.
C.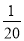 D.
D. 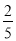
 C
【解析】【解析】
全部是20名团员,抽取1名,所以被抽到的概率是,故选C。
C
【解析】【解析】
全部是20名团员,抽取1名,所以被抽到的概率是,故选C。 如图,已知在△ABC中,AD⊥BC于点D,AE平分∠BAC,判断∠EAD与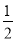 (∠C-∠B)的关系,并说明理由.
(∠C-∠B)的关系,并说明理由.
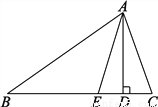
 ∠EAD= (∠C-∠B).理由见解析
【解析】试题分析:根据三角形内角和定理求出求出∠DAC和∠EAC,相减即可得出答案.
试题解析:
理由是:
∵AE平分∠BAC,
∵AD⊥BC,
∠EAD= (∠C-∠B).理由见解析
【解析】试题分析:根据三角形内角和定理求出求出∠DAC和∠EAC,相减即可得出答案.
试题解析:
理由是:
∵AE平分∠BAC,
∵AD⊥BC, 下列条件中,能判定△ABC为直角三角形的是( )
A. ∠A=∠B=∠C B. ∠A+∠B=2∠C
C. ∠A∶∠B∶∠C=1∶2∶3 D. ∠A=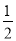 ∠B=
∠B=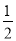 ∠C
∠C
 C
【解析】试题解析:A. ,∠A=∠B=∠C不能确定△ABC为直角三角形,所以A选项错误;
B. ,而∠A+∠B=2∠C,则所以B选项错误;
C. ,而∠A∶∠B∶∠C=1∶2∶3,则,所以C选项正确;
D. ,而则所以D选项错误.
故选C.
C
【解析】试题解析:A. ,∠A=∠B=∠C不能确定△ABC为直角三角形,所以A选项错误;
B. ,而∠A+∠B=2∠C,则所以B选项错误;
C. ,而∠A∶∠B∶∠C=1∶2∶3,则,所以C选项正确;
D. ,而则所以D选项错误.
故选C. 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.
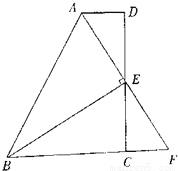
 (1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)根据线段垂直平分线的性质判断出AB=BF即可.
证明:(1)∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点...
(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)根据线段垂直平分线的性质判断出AB=BF即可.
证明:(1)∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点... 如图,△ABC,△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上,试说明:△CDA≌△CEB.
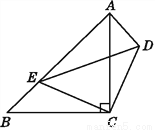
 答案见解析
【解析】试题分析:根据等腰直角三角形的性质得出CE=CD,BC=AC,再利用全等三角形的判定证明即可.
试题解析:证明:∵△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,
∴CE=CD,BC=AC,
∴∠ACB﹣∠ACE=∠DCE﹣∠ACE,
∴∠ECB=∠DCA,
在△CDA与△CEB中, ,
∴△CDA≌△CEB.
答案见解析
【解析】试题分析:根据等腰直角三角形的性质得出CE=CD,BC=AC,再利用全等三角形的判定证明即可.
试题解析:证明:∵△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,
∴CE=CD,BC=AC,
∴∠ACB﹣∠ACE=∠DCE﹣∠ACE,
∴∠ECB=∠DCA,
在△CDA与△CEB中, ,
∴△CDA≌△CEB. 阅读下面的证明过程,指出其错误.
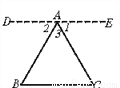
已知△ABC
求证:∠A+∠B+∠C=180°
证明:过A作DE∥BC,且使∠1=∠C
∵DE∥BC(画图)
∴∠2=∠B(两直线平行,内错角相等)
∵∠1=∠C(画图)
∴∠B+∠C+∠3=∠2+∠1+∠3=180°
即∠BAC+∠B+∠C=180°
 答案见解析
【解析】试题分析:注意作辅助线的方法,过点A作的辅助线不能同时满足两个条件.只能作平行线后,根据平行线的性质得到∠1=∠C.
错误①:过A作DE∥BC,且使∠1=∠C,应改为:过A作DE∥BC.
错误②:∵∠1=∠C(画图),理由错,应改为:两直线平行,内错角相等.
答案见解析
【解析】试题分析:注意作辅助线的方法,过点A作的辅助线不能同时满足两个条件.只能作平行线后,根据平行线的性质得到∠1=∠C.
错误①:过A作DE∥BC,且使∠1=∠C,应改为:过A作DE∥BC.
错误②:∵∠1=∠C(画图),理由错,应改为:两直线平行,内错角相等. 
