题目内容
下列条件中,能判定△ABC为直角三角形的是( )
A. ∠A=∠B=∠C B. ∠A+∠B=2∠C
C. ∠A∶∠B∶∠C=1∶2∶3 D. ∠A=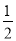 ∠B=
∠B=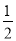 ∠C
∠C
 C
【解析】试题解析:A. ,∠A=∠B=∠C不能确定△ABC为直角三角形,所以A选项错误;
B. ,而∠A+∠B=2∠C,则所以B选项错误;
C. ,而∠A∶∠B∶∠C=1∶2∶3,则,所以C选项正确;
D. ,而则所以D选项错误.
故选C.
C
【解析】试题解析:A. ,∠A=∠B=∠C不能确定△ABC为直角三角形,所以A选项错误;
B. ,而∠A+∠B=2∠C,则所以B选项错误;
C. ,而∠A∶∠B∶∠C=1∶2∶3,则,所以C选项正确;
D. ,而则所以D选项错误.
故选C.
练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
下面四个图形中,线段BE是△ABC的高的图是( )
A. 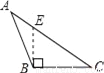 B.
B. 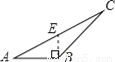 C.
C. 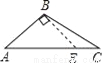 D.
D. 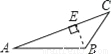
 D
【解析】试题分析:根据三角形高的画法知,过点B作AC边上的高,垂足为E,其中线段BE是△ABC的高,再结合图形进行判断.
【解析】
线段BE是△ABC的高的图是选项D.
故选D.
D
【解析】试题分析:根据三角形高的画法知,过点B作AC边上的高,垂足为E,其中线段BE是△ABC的高,再结合图形进行判断.
【解析】
线段BE是△ABC的高的图是选项D.
故选D. 在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A | 必然事件 | 随机事件 |
m的值 |
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个球是黑球的可能性大小是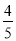 ,求m的值.
,求m的值.
 (1)填表见解析;(2)2.
【解析】试题分析:(1)当袋子中全部为黑球时,摸出黑球才是必然事件,否则就是随机事件;
(2)利用概率公式列出方程,求得m的值即可.
试题解析:(1)当袋子中全为黑球,即摸出4个红球时,摸到黑球是必然事件;
当摸出2个或3个时,摸到黑球为随机事件,
故答案为:4;2,3.
(2)根据题意得: ,
解得:m=2,
所以m的...
(1)填表见解析;(2)2.
【解析】试题分析:(1)当袋子中全部为黑球时,摸出黑球才是必然事件,否则就是随机事件;
(2)利用概率公式列出方程,求得m的值即可.
试题解析:(1)当袋子中全为黑球,即摸出4个红球时,摸到黑球是必然事件;
当摸出2个或3个时,摸到黑球为随机事件,
故答案为:4;2,3.
(2)根据题意得: ,
解得:m=2,
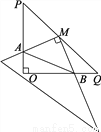
所以m的... 如图,在Rt△POQ中,OP=OQ=4,M是PQ中点,∠P=∠Q=45°,将一三角尺的直角顶点放在点M处,以M为旋转中心旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.试说明:MA=MB.
 +
+
 说明见解析
【解析】试题分析:过点M作ME⊥PO,MF⊥QO,可得四边形OEBF是矩形,根据三角形的中位线定理可得ME=MF,再根据同角的余角相等可得再利用“角边角”证明和全等,根据全等三角形对应边相等即可证明;
试题解析:过点M作ME⊥PO,MF⊥QO,
∴∠PEM=∠QFM=90°,又∵∠P=∠Q=45°,
∴∠PME=∠QMF=45°,∠EMF=90°,
又∵P...
说明见解析
【解析】试题分析:过点M作ME⊥PO,MF⊥QO,可得四边形OEBF是矩形,根据三角形的中位线定理可得ME=MF,再根据同角的余角相等可得再利用“角边角”证明和全等,根据全等三角形对应边相等即可证明;
试题解析:过点M作ME⊥PO,MF⊥QO,
∴∠PEM=∠QFM=90°,又∵∠P=∠Q=45°,
∴∠PME=∠QMF=45°,∠EMF=90°,
又∵P... 长为l的一根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边x的取值范围为__________.
 ≤x<
【解析】试题解析:∵围成两个全等的三角形可得两个三角形的周长相等,
∴可得
又因为x为最长边大于周长的,
综上可得
故答案为:
≤x<
【解析】试题解析:∵围成两个全等的三角形可得两个三角形的周长相等,
∴可得
又因为x为最长边大于周长的,
综上可得
故答案为: 锐角三角形中,最大角α的取值范围是( )
A. 0°< α < 90° B. 60°< α < 180° C. 60°< α < 90° D. 60°≤α < 90°
 D
【解析】试题分析:根据三角形的内角和定理,又α是最大角,得:3α≥180°,即α≥60°,故最大角α的取值范围是60°≤α<180度.
D
【解析】试题分析:根据三角形的内角和定理,又α是最大角,得:3α≥180°,即α≥60°,故最大角α的取值范围是60°≤α<180度. 如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于 AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
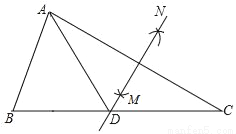
A. 65° B. 60° C. 55° D. 45°
 A
【解析】分析:根据线段垂直平分线的性质得到AD=DC,根据等腰三角形的性质得到∠C=∠DAC,
求得∠DAC=30°,根据三角形的内角和得到∠BAC=95°,即可得到结论.
详解:由题意可得:MN是AC的垂直平分线,则AD=DC,故∠C=∠DAC.
∵∠C=30°,∴∠DAC=30°.
∵∠B=55°,∴∠BAC=95°,∴∠BAD=∠BAC﹣∠CAD=65°.
...
A
【解析】分析:根据线段垂直平分线的性质得到AD=DC,根据等腰三角形的性质得到∠C=∠DAC,
求得∠DAC=30°,根据三角形的内角和得到∠BAC=95°,即可得到结论.
详解:由题意可得:MN是AC的垂直平分线,则AD=DC,故∠C=∠DAC.
∵∠C=30°,∴∠DAC=30°.
∵∠B=55°,∴∠BAC=95°,∴∠BAD=∠BAC﹣∠CAD=65°.
... 如图,过正方形ABCD的顶点B作直线l,过点A,C作l的垂线,垂足分别为点E,F.若AE=2,CF=6,则AB的长度为 .
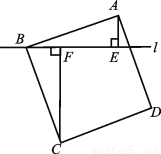
 .
【解析】
试题分析:∵四边形ABCD是正方形,
∴∠CBF+∠FBA=90°,∠CBF+∠BCF=90°,
∴∠BCF=∠ABE,
∵∠AEB=∠BFC=90°,AB=BC,
∴△ABE≌△BCF(AAS)
∴AE=BF,BE=CF,
∴AB=.
故答案是.
.
【解析】
试题分析:∵四边形ABCD是正方形,
∴∠CBF+∠FBA=90°,∠CBF+∠BCF=90°,
∴∠BCF=∠ABE,
∵∠AEB=∠BFC=90°,AB=BC,
∴△ABE≌△BCF(AAS)
∴AE=BF,BE=CF,
∴AB=.
故答案是. 如图,已知AB∥CD,∠B=65°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.
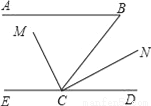
 32.5°.
【解析】试题分析:已知AB∥CD,∠B=65°,根据平行线的性质可求得∠BCE =115°;再由角平分线的定义求得∠ECM的度数,即可求得∠DCN的度数.
试题解析:
∵ AB∥CD,∴ ∠B+∠BCE =180°(两直线平行,同旁内角互补)
∵ ∠B =65°,∴ ∠BCE =115°
∵ CM平分∠BCE,∴ ∠ECM=∠BCE =57.5°
...
32.5°.
【解析】试题分析:已知AB∥CD,∠B=65°,根据平行线的性质可求得∠BCE =115°;再由角平分线的定义求得∠ECM的度数,即可求得∠DCN的度数.
试题解析:
∵ AB∥CD,∴ ∠B+∠BCE =180°(两直线平行,同旁内角互补)
∵ ∠B =65°,∴ ∠BCE =115°
∵ CM平分∠BCE,∴ ∠ECM=∠BCE =57.5°
... 
