题目内容
如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.
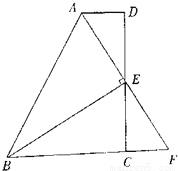
 (1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)根据线段垂直平分线的性质判断出AB=BF即可.
证明:(1)∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点...
(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)根据线段垂直平分线的性质判断出AB=BF即可.
证明:(1)∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点...
满足下列条件的△ABC中,不是直角三角形的是( )
A.∠B+∠A=∠C B.∠A:∠B:∠C=2:3:5
C.∠A=2∠B=3∠C D.一个外角等于和它相邻的一个内角
 C
【解析】本题考查了直角三角形的判定
根据三角形的内角和是及邻补角是,对各选项进行分析即可。
A、∵∠B+∠A=∠C,∴∠C=90°,∴△ABC是直角三角形;
B、∵∠A:∠B:∠C=2:3:5,∴∠C=90°,∴△ABC是直角三角形;
C、∵∠A=2∠B=3∠C,∴∠A≠90°,∴△ABC不是直角三角形;
D、∵一个外角等于和它相邻的内角,∴每一个角等于90...
C
【解析】本题考查了直角三角形的判定
根据三角形的内角和是及邻补角是,对各选项进行分析即可。
A、∵∠B+∠A=∠C,∴∠C=90°,∴△ABC是直角三角形;
B、∵∠A:∠B:∠C=2:3:5,∴∠C=90°,∴△ABC是直角三角形;
C、∵∠A=2∠B=3∠C,∴∠A≠90°,∴△ABC不是直角三角形;
D、∵一个外角等于和它相邻的内角,∴每一个角等于90... 端午节吃粽子是中华民族的传统习俗,妈妈买了2只红豆粽、3只碱水粽、5只干肉粽,粽子除内部馅料不同外其它均相同,小颖随意吃一个,吃到红豆粽的概率是( )
A. 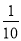 B.
B. 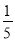 C.
C. 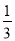 D.
D. 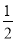
 B
【解析】试题分析:根据概率的定义,一共有10只粽子,其中红豆粽有2个,所以吃到红豆粽的概率是.
故选:B.
B
【解析】试题分析:根据概率的定义,一共有10只粽子,其中红豆粽有2个,所以吃到红豆粽的概率是.
故选:B. 长为l的一根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边x的取值范围为__________.
 ≤x<
【解析】试题解析:∵围成两个全等的三角形可得两个三角形的周长相等,
∴可得
又因为x为最长边大于周长的,
综上可得
故答案为:
≤x<
【解析】试题解析:∵围成两个全等的三角形可得两个三角形的周长相等,
∴可得
又因为x为最长边大于周长的,
综上可得
故答案为: 如图,线段AD把△ABC分为面积相等的两部分,则线段AD是( ).
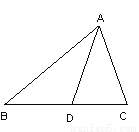
A. 三角形的角平分线 B. 三角形的中线
C. 三角形的高 D. 以上都不对
 B
【解析】试题分析:三角形的中线将三角形的面积分成相等的两部分,角平分线是指将角分成度数相等的两个角.
B
【解析】试题分析:三角形的中线将三角形的面积分成相等的两部分,角平分线是指将角分成度数相等的两个角. 如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于 AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
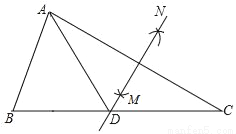
A. 65° B. 60° C. 55° D. 45°
 A
【解析】分析:根据线段垂直平分线的性质得到AD=DC,根据等腰三角形的性质得到∠C=∠DAC,
求得∠DAC=30°,根据三角形的内角和得到∠BAC=95°,即可得到结论.
详解:由题意可得:MN是AC的垂直平分线,则AD=DC,故∠C=∠DAC.
∵∠C=30°,∴∠DAC=30°.
∵∠B=55°,∴∠BAC=95°,∴∠BAD=∠BAC﹣∠CAD=65°.
...
A
【解析】分析:根据线段垂直平分线的性质得到AD=DC,根据等腰三角形的性质得到∠C=∠DAC,
求得∠DAC=30°,根据三角形的内角和得到∠BAC=95°,即可得到结论.
详解:由题意可得:MN是AC的垂直平分线,则AD=DC,故∠C=∠DAC.
∵∠C=30°,∴∠DAC=30°.
∵∠B=55°,∴∠BAC=95°,∴∠BAD=∠BAC﹣∠CAD=65°.
... 下列说法中:
①P是线段AB上的一点,直线l经过点P且l⊥AB,则l是线段AB的垂直平分线;
②直线l经过线段AB的中点,则l是线段AB的垂直平分线;
③若AP=PB,且直线l垂直于线段AB,则l是线段AB的垂直平分线;
④经过线段AB的中点P且垂直于AB的直线l是线段AB的垂直平分线.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
 A
【解析】根据线段的垂直平分线的定义,以及定理:到线段的两端距离相等的点在线段的垂直平分线上,即可判断.
【解析】
①当P不是AB的中点,则直线l不平分线段AB,故错误;
②直线l经过线段AB的中点,且垂直于AB则l是线段AB的垂直平分线,故错误;
③若AP=PB,则P在线段AB的垂直平分线上,但l不一定过点P,所以直线l不一定是线段AB的垂直平分线,故错误;
④...
A
【解析】根据线段的垂直平分线的定义,以及定理:到线段的两端距离相等的点在线段的垂直平分线上,即可判断.
【解析】
①当P不是AB的中点,则直线l不平分线段AB,故错误;
②直线l经过线段AB的中点,且垂直于AB则l是线段AB的垂直平分线,故错误;
③若AP=PB,则P在线段AB的垂直平分线上,但l不一定过点P,所以直线l不一定是线段AB的垂直平分线,故错误;
④... 在△ABC中,∠C=90°,cosA=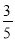 ,AC=6.求△ABC的周长和面积.
,AC=6.求△ABC的周长和面积.
 周长为24,面积为24.
【解析】试题分析:根据余弦的定义求出斜边AB的长,再根据勾股定理求出BC的长,再根据三角形的周长、面积的求法即可得.
试题解析:∵∠C=90°,∴cosA=,
∵cosA=,AC=6,
∴AB=10,
∴BC==8,
∴△ABC的周长=AC+BC+AB=6+8+10=24,
S△ABC==24.
周长为24,面积为24.
【解析】试题分析:根据余弦的定义求出斜边AB的长,再根据勾股定理求出BC的长,再根据三角形的周长、面积的求法即可得.
试题解析:∵∠C=90°,∴cosA=,
∵cosA=,AC=6,
∴AB=10,
∴BC==8,
∴△ABC的周长=AC+BC+AB=6+8+10=24,
S△ABC==24. 下列命题正确的是( )
A.内错角相等
B.相等的角是对顶角
C.三条直线相交 ,必产生同位角、内错角、同旁内角
D.同位角相等,两直线平行
 D.
【解析】
试题分析:A.只有两直线平行,内错角才相等,故错误;
B.对顶角相等,但相等的角不一定是对顶角,故错误;
C.必须出现“三线八角”的形式,即两直线被第三条直线所截,才产生同位角,内错角,同旁内角,故错误;
D.平行线的判定定理,故正确.
故选D.
D.
【解析】
试题分析:A.只有两直线平行,内错角才相等,故错误;
B.对顶角相等,但相等的角不一定是对顶角,故错误;
C.必须出现“三线八角”的形式,即两直线被第三条直线所截,才产生同位角,内错角,同旁内角,故错误;
D.平行线的判定定理,故正确.
故选D. 
