��Ŀ����
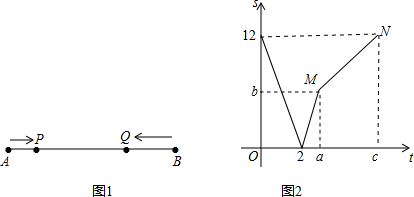
14����ͼ1���߶�AB=12���ף�����P�ӵ�A�������B�˶�������Q�ӵ�B�������A�˶�������ͬʱ������������Ե��յ��ֹͣ�˶�����֪����Q�˶����ٶ��Ƕ���P�˶����ٶȵ�2����������֮��ľ���Ϊs�����ף�������P���˶�ʱ��Ϊt���룩��ͼ2��ʾs��t֮��ĺ�����ϵ����1����P��Q�˶����ٶȣ�
��2��ͼ2�У�a=3��b=6��c=6��
��3����a��t��cʱ����s��t֮��ĺ�����ϵʽ�����߶�MN��Ӧ�ĺ�����ϵʽ����
���� ��1���趯��P�˶����ٶ�Ϊx����/�룬��Q�˶����ٶ�Ϊ2x����/�룬����ͼ���֪����2������֮��ľ���Ϊ0��������2��������������������ʱ�������˶���·��֮��=12�����г����̣���⼴�ɣ�
��2������ͼ���֪��a��ֵΪ����Q�ӵ�B�˶�����A��ʱ�䣬����ʱ��=·�̡��ٶ���ʽ���a=3��b��ֵΪ����P�˶�3��ʱ��·�̣�����·��=�ٶȡ�ʱ����ʽ��⣻c��ֵΪ����P�ӵ�A�˶�����B��ʱ�䣬����ʱ��=·�̡��ٶ���ʽ��⣻
��3����3��t��6ʱ����s��t֮��ĺ�����ϵʽΪs=kt+b������3��6������6��12�����룬���ô���ϵ����������⣮
��� �⣺��1���趯��P�˶����ٶ�Ϊx����/�룬��Q�˶����ٶ�Ϊ2x����/�룬
�������⣬��2��x+2x��=12��
���x=2��
�𣺶���P��Q�˶����ٶȷֱ���2����/�롢4����/�룻
��2������Q�˶���ʱ��a=$\frac{12}{4}$=3��
����3�룬����Q�ӵ�B�˶�����A����ʱ����P�˶���·��Ϊ2��3=6����b=6��
����P�˶���ʱ��c=$\frac{12}{2}$=6��
�ʴ�Ϊ3��6��6��
��3����3��t��6ʱ����s��t֮��ĺ�����ϵʽΪs=kt+b��
��ͼ����㣨3��6������6��12����
��$\left\{\begin{array}{l}{3k+b=6}\\{6k+b=12}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=2}\\{b=0}\end{array}\right.$��
��s��t֮��ĺ�����ϵʽΪs=2t��3��t��6����
���� ���⿼���˶�������ĺ���ͼ��·�̡��ٶ���ʱ��Ĺ�ϵ������ϵ������һ�κ����Ľ���ʽ��֪ʶ�㣮����ؼ�����������ĺ���ͼ���˽�ͼ���йؼ�����������ʵ�����壬�����������˶����̣�

 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�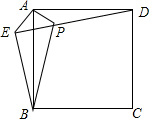 ��֪����ͼ����������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�ED�ڵ�P����AE=AP=1��PB=$\sqrt{5}$�����н��ۣ�
��֪����ͼ����������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�ED�ڵ�P����AE=AP=1��PB=$\sqrt{5}$�����н��ۣ��١�APD�ա�AEB��
�ڵ�B��ֱ��AE�ľ���Ϊ$\sqrt{2}$��
��EB��ED��
��S������ABCD=4+$\sqrt{6}$��
��S��APD+S��APB=1+$\sqrt{6}$��
������ȷ���۵�����ǣ�������
| A�� | �٢ۢ� | B�� | �٢ڢ� | C�� | �ۢܢ� | D�� | �٢ۢ� |
 ��ͼ��ֱ��a��b����1=37�㣬���2�Ķ����ǣ�������
��ͼ��ֱ��a��b����1=37�㣬���2�Ķ����ǣ�������| A�� | 57�� | B�� | 37�� | C�� | 143�� | D�� | 53�� |
 ��ͼ��EO��AB��O��ֱ��CD��O�㣬��EOD����EOB=1��3�����AOC����AOE�Ķ�����
��ͼ��EO��AB��O��ֱ��CD��O�㣬��EOD����EOB=1��3�����AOC����AOE�Ķ�����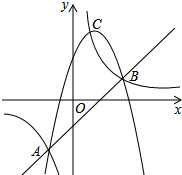 ��֪Y1��Y2��Y3�ֱ��ʾ���κ�����������������һ�κ�������������ֵ�����ǵĽ���ֱ���A��-1��-2����B��2��1����C��$\frac{2}{3}$��3�����涨M={Y1��Y2��Y3����С�ĺ���ֵ}�������н��ۣ�
��֪Y1��Y2��Y3�ֱ��ʾ���κ�����������������һ�κ�������������ֵ�����ǵĽ���ֱ���A��-1��-2����B��2��1����C��$\frac{2}{3}$��3�����涨M={Y1��Y2��Y3����С�ĺ���ֵ}�������н��ۣ�