题目内容
7.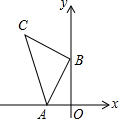 如图,在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,n),以点B为直角顶点,点C在第二象限内,作等腰直角△ABC.则点C的坐标是(-n,2+n).(用字母n表示).
如图,在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,n),以点B为直角顶点,点C在第二象限内,作等腰直角△ABC.则点C的坐标是(-n,2+n).(用字母n表示).
分析 作CE⊥y轴于E,证△CEB≌△BOA,推出CE=OB=n,BE=AO=2,即可得出答案.
解答 解:(1)作CE⊥y轴于E,如图1,
∵A(-2,0),B(0,n),
∴OA=2,OB=n,
∵∠CBA=90°,
∴∠CEB=∠AOB=∠CBA=90°,
∴∠ECB+∠EBC=90°,∠CBE+∠ABO=90°,
∴∠ECB=∠ABO,
在△CBE和△BAO中
$\left\{\begin{array}{l}{∠ECB=∠ABO}\\{∠CEB=∠AOB}\\{BC=AB}\end{array}\right.$,
∴△CBE≌△BAO,
∴CE=BO=n,BE=AO=2,
即OE=2+n,
∴C(-n,2+n).
故答案为:(-n,2+n).
点评 本题考查了全等三角形的性质和判定,三角形内角和定理,等腰三角形性质的应用,主要考查学生综合运用性质进行推理的能力,用了分类讨论思想.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
15.2008年8月8日北京奥运会开幕式在国家体育场“鸟巢”举行.“鸟巢”建筑面积为2580000000cm2,数字2580000000用科学记数法表示为( )
| A. | 258×107 | B. | 25.8×108 | C. | 2.58×109 | D. | 2.58×1010 |
12.若k是方程3x+1=7的解,则4k+3的值是( )
| A. | 11 | B. | -11 | C. | 17 | D. | -7 |
16.如果关于y的整式3y2+3y-1与by2+y+b的和不含y2项,那么这个和为( )
| A. | 4y-1 | B. | 4y-2 | C. | 4y-3 | D. | 4y-4 |
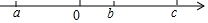 有理数a、b、c在数轴上的位置如图:化简:|b-c|+2|a+b|-|c-a|
有理数a、b、c在数轴上的位置如图:化简:|b-c|+2|a+b|-|c-a|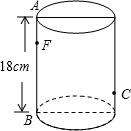 如图,圆柱形无盖玻璃容器,高18cm,底面圆的直径为$\frac{20}{π}$cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度.(结果保留根号)
如图,圆柱形无盖玻璃容器,高18cm,底面圆的直径为$\frac{20}{π}$cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度.(结果保留根号)