��Ŀ����
�о����⾭�����������һ��ķ���������ѧѧϰ�����У�ͨ�����������е�֪ʶ�뾭�飬ͨ�����о�����
���й۲졢ʵ�顢���������������������ѧ���ɣ���ʾ�о�����ı���������
��1���Ƚ����и�ʽ�Ĵ�С��
��
��
��
��2���Ƚ�ԭ��ÿ��������Ӧ�·����Ĵ�С�����Եó�����Ľ��ۣ�
һ���������
��a��b��Ϊ��������������ӷ�ĸͬ��һ������m����
�������������Ĵ�С��ϵ��
��
������������������2���н��۵ĺ��壺 ��
������ͼ�ε����˵��������ۣ�
���й۲졢ʵ�顢���������������������ѧ���ɣ���ʾ�о�����ı���������
��1���Ƚ����и�ʽ�Ĵ�С��
| 1 |
| 3 |
| 1+1 |
| 3+1 |
| 2 |
| 5 |
| 2+1 |
| 5+1 |
| 3 |
| 4 |
| 3+1 |
| 4+1 |
��2���Ƚ�ԭ��ÿ��������Ӧ�·����Ĵ�С�����Եó�����Ľ��ۣ�
һ���������
| a |
| b |
| a+m |
| b+m |
| a+m |
| b+m |
| a |
| b |
������������������2���н��۵ĺ��壺
������ͼ�ε����˵��������ۣ�
���㣺��ʽ�Ļ������
ר�⣺�Ķ���
��������1���ұ�ʽ�Ӽ���õ���������������жϣ�
��2�������ܽ�õ�һ���Թ��ɣ��Ƚϼ��ɣ�
�ٸ��ݵó��Ľ���д�����ɣ�
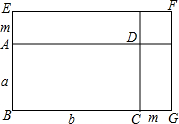
����ͼ��ʾ�����ı���BEFG��ABCD��Ϊ���Σ�����aС��b�����߳���m������ab�����κɵ�֤��
��2�������ܽ�õ�һ���Թ��ɣ��Ƚϼ��ɣ�
�ٸ��ݵó��Ľ���д�����ɣ�
����ͼ��ʾ�����ı���BEFG��ABCD��Ϊ���Σ�����aС��b�����߳���m������ab�����κɵ�֤��
��� �⣺��1����������ã�
�⣺��1����������ã�
��
��
��
��
��
��
��2��һ���������
��a��b��Ϊ��������������ӷ�ĸͬ��һ������m����
�������������Ĵ�С��ϵ��
��
��
������������������2���н��۵ĺ��壺�����ķ��ӷ�ĸ������ͬ��������������ֵ���
����ͼ��ʾ��
���ı���BEFG�Ǿ��Σ��ı���ABCD�Ǿ��Σ�a��b��
��am��bm��
��am+ab��bm+ab����a��m+b����b��m+a����
��
��
��
�ʴ�Ϊ����1����������������2�������ٷ����ķ��ӷ�ĸ������ͬ��������������ֵ���
 �⣺��1����������ã�
�⣺��1����������ã�| 1 |
| 3 |
| 1+1 |
| 3+1 |
| 2 |
| 5 |
| 2+1 |
| 5+1 |
| 3 |
| 4 |
| 3+1 |
| 4+1 |
��2��һ���������
| a |
| b |
| a+m |
| b+m |
| a+m |
| b+m |
| a |
| b |
������������������2���н��۵ĺ��壺�����ķ��ӷ�ĸ������ͬ��������������ֵ���
����ͼ��ʾ��
���ı���BEFG�Ǿ��Σ��ı���ABCD�Ǿ��Σ�a��b��
��am��bm��
��am+ab��bm+ab����a��m+b����b��m+a����
��
| a |
| b |
| a+m |
| b+m |
�ʴ�Ϊ����1����������������2�������ٷ����ķ��ӷ�ĸ������ͬ��������������ֵ���
���������⿼���˷�ʽ�Ļ�����㣬�����������㷨���ǽⱾ��Ĺؼ���

��ϰ��ϵ�д�
 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
�����Ŀ
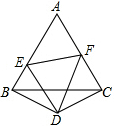 ��ͼ��D�ǵȱߡ�ABC���һ�㣬DB=DC����BDC=120�㣬��E��F�ֱ���AB��AC�ϣ�
��ͼ��D�ǵȱߡ�ABC���һ�㣬DB=DC����BDC=120�㣬��E��F�ֱ���AB��AC�ϣ�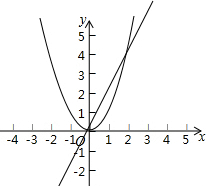 ��ͼ��ʾ��������y=x2��ֱ��y=2x�ڵ�һ��������һ������A��
��ͼ��ʾ��������y=x2��ֱ��y=2x�ڵ�һ��������һ������A��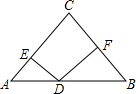 ��ͼ���ڵ���������ACB�У�AC=BC=5��AB=8��DΪ�ױ�AB��һ���㣨�����A��B�غϣ���DE��AC��DF��BC������ֱ�ΪE��F��
��ͼ���ڵ���������ACB�У�AC=BC=5��AB=8��DΪ�ױ�AB��һ���㣨�����A��B�غϣ���DE��AC��DF��BC������ֱ�ΪE��F��