题目内容
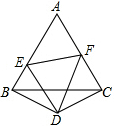 如图,D是等边△ABC外的一点,DB=DC,∠BDC=120°,且E、F分别在AB和AC上.
如图,D是等边△ABC外的一点,DB=DC,∠BDC=120°,且E、F分别在AB和AC上.(1)求证:AD是BC的垂直平分线;
(2)若ED平分∠BEF,证明:
①FD平分∠EFC;
②△AEF的周长是BC长的2倍.
考点:角平分线的性质,线段垂直平分线的性质,等边三角形的性质
专题:证明题
分析:(1)求出AB=AC,BD=DC,根据线段垂直平分线性质求出即可;
(2)①过D作DM⊥EF,连接AD,求出AD平分∠BAC,求出∠ABC=∠ACB=60°,求出BD=DM,BD=DC,推出DM=DC即可;
②求出DB=DM,DM=DC,∠EBD=∠EMD=90°,证出△EBD≌△EMD,推出EM=BE,同理FC=FM,求出EF=BE+CF,即可得出答案.
(2)①过D作DM⊥EF,连接AD,求出AD平分∠BAC,求出∠ABC=∠ACB=60°,求出BD=DM,BD=DC,推出DM=DC即可;
②求出DB=DM,DM=DC,∠EBD=∠EMD=90°,证出△EBD≌△EMD,推出EM=BE,同理FC=FM,求出EF=BE+CF,即可得出答案.
解答:证明:(1)∵△ABC是等边三角形,
∴AB=AC,
∴A在BC的垂直平分线上,
∵BD=DC,
∴D在BC的垂直平分线上,
∴AD是BC的垂直平分线;
(2)①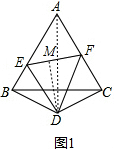
过D作DM⊥EF,连接AD,
∵AD是BC的垂直平分线,
∴AD平分∠BAC,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵BD=DC,∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠ABD=∠ACD=90°,
∴DB⊥AB,DC⊥AC,
∵DM⊥EF,ED平分∠BEF,AD平分∠BAC,
∴BD=DM,BD=DC,
∴DM=DC,
∴FD平分∠EFC;
②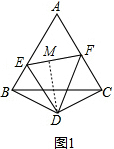
∵DE平分∠BEF,DB⊥AB,DM⊥EF,DF平分∠CFE,
∴DB=DM,DM=DC,∠EBD=∠EMD=90°,
在△EBD和△EMD中
,
∴△EBD≌△EMD,
∴EM=BE,
同理FC=FM,
∴EF=BE+CF,
∴△AEF的周长是AE+EF+AF=AE+BE+CF+AF=2AB=2BC.
∴AB=AC,
∴A在BC的垂直平分线上,
∵BD=DC,
∴D在BC的垂直平分线上,
∴AD是BC的垂直平分线;
(2)①

过D作DM⊥EF,连接AD,
∵AD是BC的垂直平分线,
∴AD平分∠BAC,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵BD=DC,∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠ABD=∠ACD=90°,
∴DB⊥AB,DC⊥AC,
∵DM⊥EF,ED平分∠BEF,AD平分∠BAC,
∴BD=DM,BD=DC,
∴DM=DC,
∴FD平分∠EFC;
②

∵DE平分∠BEF,DB⊥AB,DM⊥EF,DF平分∠CFE,
∴DB=DM,DM=DC,∠EBD=∠EMD=90°,
在△EBD和△EMD中
|
∴△EBD≌△EMD,
∴EM=BE,
同理FC=FM,
∴EF=BE+CF,
∴△AEF的周长是AE+EF+AF=AE+BE+CF+AF=2AB=2BC.
点评:此题考查了等边三角形,直角三角形,等腰三角形的性质以及全等三角形的判定与性质等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想的应用与辅助线的作法.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
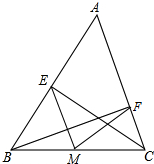 如图所示:CE,BF是△ABC的两条高,M是BC的中点,连ME,MF,∠BAC=50°,则∠EMF的大小是( )
如图所示:CE,BF是△ABC的两条高,M是BC的中点,连ME,MF,∠BAC=50°,则∠EMF的大小是( )| A、50° | B、60° |
| C、70° | D、80° |
从一付没有大小王的扑克中任意抽出一张,抽到红心的机会是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知∠B=∠C=∠BAD,∠ADC=∠DAC,AE⊥BC,求∠DAE的度数.
如图,已知∠B=∠C=∠BAD,∠ADC=∠DAC,AE⊥BC,求∠DAE的度数.