Question

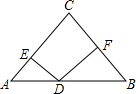如图，在等腰三角形ACB中，AC=BC=5，AB=8，D为底边AB上一动点（不与点A，B重合），DE⊥AC，DF⊥BC，垂足分别为E，F，
（1）求DE+DF的长．
（2）若点D在AB的延长线上，（1）中的结论还成立吗？请说明理由．

Answer 1

考点：等腰三角形的性质

专题：

分析：（1）连接CD，过C点作底边AB上的高CG，根据S_△ABC=S_△ACD+S_△DCB不难求得DE+DF=4.8．
（2）连接CD，过C点作底边AB上的高CG，根据S_△ABC=S_△ACD-S_△DCB求得DE-DF=4.8，从而判断（1）中的结论不成立．

解答：解：（1）如图1，连接CD，过C点作底边AB上的高CG，
∵AC=BC=5，AB=8，
∴BG=4，CG=

BC2-BG2

=

52-42

=3，
∵S_△ABC=S_△ACD+S_△DCB，
∴AB•CG=AC•DE+BC•DF，
∵AC=BC，
∴8×3=5×（DE+DF）
∴DE+DF=4.8．

（2）不成立，
如图2，连接CD，过C点作底边AB上的高CG，
∵AC=BC=5，AB=8，
∴BG=4，CG=

BC2-BG2

=

52-42

=3，
∵S_△ABC=S_△ACD-S_△DCB，
∴AB•CG=AC•DE-BC•DF，
∵AC=BC，
∴8×3=5×（DE-DF）
∴DE-DF=4.8．
故若点D在AB的延长线上，（1）中的结论不成立．

点评：本题考查了等腰三角形的性质，辅助线是解决几何问题的一个关键，还考查了等腰三角形“三线合一”的性质．