题目内容
13.一列快车长306m,一列慢车长344m,两车相向而行,从相遇到离开需要13s,如果同向而行,快车从追及到超过慢车需要65s,求快车、慢车各自的速度.若设快车速度为x m/s,慢车速度为y m/s,那么,由题意列出的方程为( )| A. | $\left\{\begin{array}{l}13(x+y)=306+344\\ 65(x-y)=344\end{array}$ | B. | $\left\{\begin{array}{l}13(x+y)=306+344\\ 65(x-y)=344+306\end{array}$ | ||
| C. | $\left\{\begin{array}{l}13(x+y)=306+344\\ 65(x-y)=344-306\end{array}$ | D. | $\left\{\begin{array}{l}344y=306x\\ 65(x-y)=344+306\end{array}$ |
分析 设快车速度为x m/s,慢车速度为y m/s,根据题意可得,两车相向而行,用13s走了(344+306)米,快车追击慢车,用65s走了(344+306)米,据此列方程组.
解答 解:设快车速度为x m/s,慢车速度为y m/s,
由题意得,$\left\{\begin{array}{l}{13(x+y)=306+344}\\{65(x-y)=344+306}\end{array}\right.$.
故选B.
点评 本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
4.已知∠A,∠B,∠C均为锐角,若tanA>$\sqrt{3}$,sinB<$\frac{1}{2}$,cosC=$\frac{\sqrt{2}}{2}$,则( )
| A. | ∠A>∠B>∠C | B. | ∠C>∠B>∠A | C. | ∠B>∠C>∠A | D. | ∠A>∠C>∠B |
1.如果∠A是锐角,且sinA=$\frac{3}{4}$,那么∠A的范围是( )
| A. | 0°<∠A<30° | B. | 30°<∠A<45° | C. | 45°<∠A<60° | D. | 60°<∠A<90° |
5.某商店出售某商品时,在进价的基础上加一定的利润,其数量x与售价y的关系如下表所示.请根据表中所提供的信息,列出y与x之间的函数关系式,并求出当数量是2.5千克时的售价.
| 数量x(千克) | 1 | 2 | 3 | 4 | … |
| 售价y(元) | 8+0.4 | 16+0.8 | 24+1.2 | 32+1.6 | … |
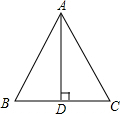 在△ABC中,AB=AC,AD是底边上的高,如图,若AC=6cm,AD=5cm,求BD的值.(精确到0.01cm)
在△ABC中,AB=AC,AD是底边上的高,如图,若AC=6cm,AD=5cm,求BD的值.(精确到0.01cm)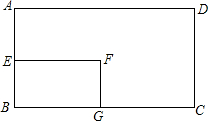 如图,矩形ABCD的面积是72,AE=$\frac{1}{2}$DC,EF=$\frac{1}{2}$AD,那么矩形EBGF的面积是( )
如图,矩形ABCD的面积是72,AE=$\frac{1}{2}$DC,EF=$\frac{1}{2}$AD,那么矩形EBGF的面积是( )