题目内容
3．
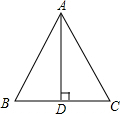在△ABC中，AB=AC，AD是底边上的高，如图，若AC=6cm，AD=5cm，求BD的值．（精确到0.01cm）
分析 先根据勾股定理求出CD的长，再由等腰三角形的性质即可得出结论．
解答 解：∵AC=6cm，AD=5cm，AD⊥BC，
∴CD=$\sqrt{{AC}^{2}-{AD}^{2}}$=$\sqrt{{6}^{2}-{5}^{2}}$=$\sqrt{36-25}$=$\sqrt{11}$≈3.32（cm）．
∵AB=AC，
∴BD=CD=3.32（cm）．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
13．若△ABC和△DEF满足下列条件，其中使△ABC与△DEF相似的是（ ）
| A． | AB=6，BC=6，AC=9，DE=4，EF=4，DF=6 | |
| B． | AB=4，BC=6，AC=8，DE=5，EF=10，DF=15 | |
| C． | AB=1，BC=$\sqrt{2}$，AC=2，DE=$\sqrt{6}$，EF=$\sqrt{3}$，DF=$\sqrt{5}$ | |
| D． | AB=1，BC=$\sqrt{5}$，AC=3，DE=$\sqrt{15}$，EF=2$\sqrt{3}$，DF=$\sqrt{6}$ |
14．电影院的第3排第6座表示为（3，6）．若某同学的座位号为（4，2），那么该同学的位置是（ ）
| A． | 第2排第4座 | B． | 第4排第2座 | C． | 第4座第4排 | D． | 无法确定 |
11．
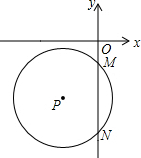如图，半径为5的⊙P与y轴交于点M（0，-4），N（0，-10），函数y=kx的图象经过点P，则k的值为（ ）
如图，半径为5的⊙P与y轴交于点M（0，-4），N（0，-10），函数y=kx的图象经过点P，则k的值为（ ）| A． | -$\frac{4}{7}$ | B． | -$\frac{7}{4}$ | C． | $\frac{4}{7}$ | D． | $\frac{7}{4}$ |
18．
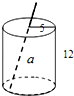如图，是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是（ ）
如图，是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是（ ）| A． | 5≤a≤12 | B． | 5≤a≤13 | C． | 12≤a≤13 | D． | 12≤a≤15 |
13．一列快车长306m，一列慢车长344m，两车相向而行，从相遇到离开需要13s，如果同向而行，快车从追及到超过慢车需要65s，求快车、慢车各自的速度．若设快车速度为x m/s，慢车速度为y m/s，那么，由题意列出的方程为（ ）
| A． | $\left\{\begin{array}{l}13（x+y）=306+344\\ 65（x-y）=344\end{array}$ | B． | $\left\{\begin{array}{l}13（x+y）=306+344\\ 65（x-y）=344+306\end{array}$ | ||
| C． | $\left\{\begin{array}{l}13（x+y）=306+344\\ 65（x-y）=344-306\end{array}$ | D． | $\left\{\begin{array}{l}344y=306x\\ 65（x-y）=344+306\end{array}$ |