题目内容
18.在同一坐标系内画出正比例函数y1=-2x与y2=$\frac{1}{2}$x的图象.分析 根据两条直线的解析式其图象均过原点,再分别令x=1求出y的值,描出各点,根据两点确定一条直线画出函数图象.
解答 解:如图:
点评 本题考查了正比例函数的图象,解答此题的关键是画出函数的图象,

练习册系列答案
相关题目
9.在Rt△ABC中,∠C=90°,tanA=$\frac{2}{3}$,AC=4,则BC等于( )
| A. | $\frac{8}{3}$ | B. | 2 | C. | 1 | D. | $\frac{7}{3}$ |
13.一列快车长306m,一列慢车长344m,两车相向而行,从相遇到离开需要13s,如果同向而行,快车从追及到超过慢车需要65s,求快车、慢车各自的速度.若设快车速度为x m/s,慢车速度为y m/s,那么,由题意列出的方程为( )
| A. | $\left\{\begin{array}{l}13(x+y)=306+344\\ 65(x-y)=344\end{array}$ | B. | $\left\{\begin{array}{l}13(x+y)=306+344\\ 65(x-y)=344+306\end{array}$ | ||
| C. | $\left\{\begin{array}{l}13(x+y)=306+344\\ 65(x-y)=344-306\end{array}$ | D. | $\left\{\begin{array}{l}344y=306x\\ 65(x-y)=344+306\end{array}$ |
10.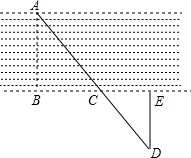 为了测量一条小河的宽度,小明所在小组同学决定选取河对岸岸边某处为A点,在同侧岸边选取B,C,E三点,使B,C,E在同一直线上,且AB与BE垂直.再过点E作DE⊥BE交AC的延长线于点D,并测得BC=15m,CE=3m,DE=5.4m,则河的宽度AB约为( )
为了测量一条小河的宽度,小明所在小组同学决定选取河对岸岸边某处为A点,在同侧岸边选取B,C,E三点,使B,C,E在同一直线上,且AB与BE垂直.再过点E作DE⊥BE交AC的延长线于点D,并测得BC=15m,CE=3m,DE=5.4m,则河的宽度AB约为( )
 为了测量一条小河的宽度,小明所在小组同学决定选取河对岸岸边某处为A点,在同侧岸边选取B,C,E三点,使B,C,E在同一直线上,且AB与BE垂直.再过点E作DE⊥BE交AC的延长线于点D,并测得BC=15m,CE=3m,DE=5.4m,则河的宽度AB约为( )
为了测量一条小河的宽度,小明所在小组同学决定选取河对岸岸边某处为A点,在同侧岸边选取B,C,E三点,使B,C,E在同一直线上,且AB与BE垂直.再过点E作DE⊥BE交AC的延长线于点D,并测得BC=15m,CE=3m,DE=5.4m,则河的宽度AB约为( )| A. | 21m | B. | 24m | C. | 27m | D. | 8.6m |
8.下列命题的逆命题正确的是( )
| A. | 若两数相等,则它们的绝对值相等 | B. | 对顶角相等 | ||
| C. | 若a≥0,则${(\sqrt{a})}^{2}$=a | D. | 全等三角形面积相等 |

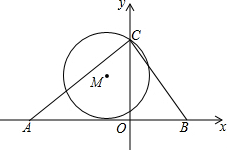 如图,在△ABC中,AB=10,AC=8,BC=6.点A、B、C都在坐标轴上.⊙M过点C且与x轴相切.设点M(x,y).
如图,在△ABC中,AB=10,AC=8,BC=6.点A、B、C都在坐标轴上.⊙M过点C且与x轴相切.设点M(x,y).