题目内容
1.计算:①$\sqrt{9}$-4×($\frac{1}{2}$)-2+|-5|+(π-3)0
②$\frac{3}{x-4}$-$\frac{24}{{x}^{2}-16}$.
分析 (1)根据负整数指数幂、绝对值、零指数幂可以解答本题;
(2)先对原式通分然后再化简即可解答本题.
解答 解:①$\sqrt{9}$-4×($\frac{1}{2}$)-2+|-5|+(π-3)0
=3-4×4+5+1
=3-16+5+1
=-7;
②$\frac{3}{x-4}$-$\frac{24}{{x}^{2}-16}$
=$\frac{3(x+4)-24}{(x-4)(x+4)}$
=$\frac{3x+12-24}{(x-4)(x+4)}$
=$\frac{3x-12}{(x-4)(x+4)}$
=$\frac{3(x-4)}{(x-4)(x+4)}$
=$\frac{3}{x+4}$.
点评 本题考查实数的运算、分式的加减法、负整数指数幂、零指数幂,解题的关键是明确它们各自的计算方法.

练习册系列答案
相关题目
12. 如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )
如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )
 如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )
如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
9.下列运算中,正确的是( )
| A. | x•x3=x3 | B. | (x2)3=x5 | C. | x6÷x2=x4 | D. | (x-y)2=x2+y2 |
6.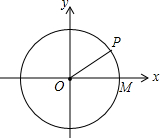 在平面直角坐标系中,以原点O为圆心的⊙O交x轴正半轴为M,P为圆上一点,坐标为($\sqrt{3}$,1),则cos∠POM=( )
在平面直角坐标系中,以原点O为圆心的⊙O交x轴正半轴为M,P为圆上一点,坐标为($\sqrt{3}$,1),则cos∠POM=( )
 在平面直角坐标系中,以原点O为圆心的⊙O交x轴正半轴为M,P为圆上一点,坐标为($\sqrt{3}$,1),则cos∠POM=( )
在平面直角坐标系中,以原点O为圆心的⊙O交x轴正半轴为M,P为圆上一点,坐标为($\sqrt{3}$,1),则cos∠POM=( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
13.下列运算正确的是( )
| A. | (2a2)3=6a6 | B. | -x6÷x2=-x4 | C. | 2x+2y=4xy | D. | (x-1)2=x2-12 |
11.下列计算正确的是( )
| A. | b3•b4=b7 | B. | (b3)4=b7 | C. | b3+b4=b7 | D. | b6÷b3=b2 |