题目内容
15．
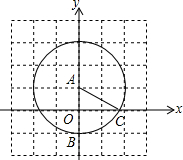如图，已知点A（0，1），B（0，-1），以点A为圆心，AB为半径作圆，交x轴的正半轴于点C，则tan∠BAC=$\sqrt{3}$．
分析 求出OA、AC，通过余弦函数即可得出答案．
解答 解：∵A（0，1），B（0，-1），
∴AB=2，OA=1，
∴AC=2，OC=$\sqrt{3}$，
在Rt△AOC中，tan∠BAC=$\frac{OC}{OA}$=$\frac{\sqrt{3}}{1}$=$\sqrt{3}$，
故答案为$\sqrt{3}$．
点评 本题考查了锐角三角函数以及垂径定理的应用，关键是求出AC、OA的长．
练习册系列答案
相关题目
甲、乙两地相距400千米，一辆货车和一辆轿车先后从甲地出发向乙地，如图，线段OA（l货）表示货车离甲地距离y（千米）与货车出发时间x（小时）之间的函数关系；折线BCD表示轿车离甲地距离y（千米）与货车出发时间x（小时）之间的函数关系，请根据图象解答下列问题：
6．
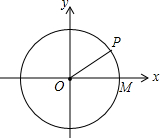在平面直角坐标系中，以原点O为圆心的⊙O交x轴正半轴为M，P为圆上一点，坐标为（$\sqrt{3}$，1），则cos∠POM=（ ）
在平面直角坐标系中，以原点O为圆心的⊙O交x轴正半轴为M，P为圆上一点，坐标为（$\sqrt{3}$，1），则cos∠POM=（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{\sqrt{2}}{2}$ |
20．下列运算正确的是（ ）
| A． | a6÷a2=a4 | B． | 2（a+b）=2a+b | C． | （ab）-2=ab-2 | D． | a3+a3=a6 |
7．下列运算正确的是（ ）
| A． | a2•a3=a6 | B． | （3a）3=9a3 | C． | a3-2a3=-1 | D． | （a2）3=a6 |
