题目内容
16.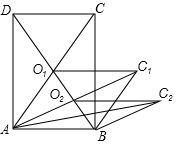 如图所示,矩形ABCD的面积为12cm2,它的两条对角线交于点O1,以AB、AO1邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2;同样以AB、AO2为邻边作平行四边形ABC2O2…;依此类推,则平行四边形ABC6O6的面积为$\frac{3}{16}$cm2.
如图所示,矩形ABCD的面积为12cm2,它的两条对角线交于点O1,以AB、AO1邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2;同样以AB、AO2为邻边作平行四边形ABC2O2…;依此类推,则平行四边形ABC6O6的面积为$\frac{3}{16}$cm2.
分析 根据矩形性质得出O1A=O1C,O1B=O1D,AC=BD,推出O1A=O1C=O1B=O1D,求出S△AO1B=$\frac{1}{2}$S△ABC=$\frac{1}{4}$S矩形ABCD=3cm2,求出四边形ABC1O1是菱形,推出AC1=2O1A,O1B=2O1O2=2O2B,AC1⊥BO1,平行四边形ABC1O1的面积是$\frac{1}{2}$AC1×BO1,推出△ABO2的面积,同理可得平行四边形ABC2O2的面积,平行四边形ABC3O3的面积,平行四边形ABC4O4的面积,平行四边形ABC5D5的面积,平行四边形ABC6O6的面积.
解答  解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴O1A=O1C,O1B=O1D,AC=BD,
∴O1A=O1C=O1B=O1D,
∴S△AO1B=$\frac{1}{2}$S△ABC=$\frac{1}{4}$S矩形ABCD=$\frac{1}{4}$×12cm2=3cm2,
∵四边形ABC1O1是平行四边形,O1A=O1B,
∴四边形ABC1O1是菱形,
∴AC1=2O2A,O1B=2O1O2=2O2B,AC1⊥BO1,
∴S?ABC1O1=$\frac{1}{2}$AC1×BO1=$\frac{1}{2}$×2AO2×BO1=2×$\frac{1}{2}$×AO2×BO1=2×3cm2=6cm2,
∴S△ABO2=$\frac{1}{4}$S?ABC1O1=$\frac{3}{2}$cm2,
同理平行四边形ABC2O2的面积是3cm2,
平行四边形ABC3O3的面积是$\frac{3}{2}$cm2,
平行四边形ABC4O4的面积是$\frac{3}{4}$cm2,
平行四边形ABC5D5的面积是$\frac{3}{8}$cm2,
平行四边形ABC6O6的面积是$\frac{3}{16}$cm2,
故答案为:$\frac{3}{16}$cm2.
点评 本题考查了矩形的性质,平行四边形性质,菱形的性质和判定,三角形的面积等知识点,解此题的关键是找出规律,题目比较好,但是有一定的难度.

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案| A. | a-2b | B. | -2ab | C. | -2 | D. | a |
| 抛掷次数n | 100 | 200 | 300 | 400 | 600 | 800 | 1000 |
| 针尖不着地的频数m | 64 | 118 | 189 | 252 | 360 | 488 | 610 |
| 针尖不着地的频数$\frac{m}{n}$ | 0.64 | 0.59 | 0.63 | 0.63 | 0.60 | 0.61 | 0.61 |
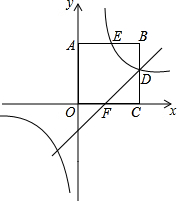 已知,正方形OABC在平面直角坐标系中的位置如图所示,点A的坐标为(0,3),双曲线y1=$\frac{k}{x}$分别交AB,BC于点E,D,直线y2=x-1过点D与x轴正半轴交于点F.
已知,正方形OABC在平面直角坐标系中的位置如图所示,点A的坐标为(0,3),双曲线y1=$\frac{k}{x}$分别交AB,BC于点E,D,直线y2=x-1过点D与x轴正半轴交于点F.