题目内容
5.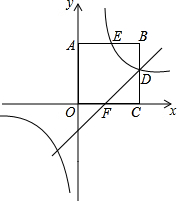 已知,正方形OABC在平面直角坐标系中的位置如图所示,点A的坐标为(0,3),双曲线y1=$\frac{k}{x}$分别交AB,BC于点E,D,直线y2=x-1过点D与x轴正半轴交于点F.
已知,正方形OABC在平面直角坐标系中的位置如图所示,点A的坐标为(0,3),双曲线y1=$\frac{k}{x}$分别交AB,BC于点E,D,直线y2=x-1过点D与x轴正半轴交于点F.(1)求反比例函数的表达式;
(2)若点P为直线y2=x-1上的一个动点,且△POF的面积与四边形AOFE的面积相等,求点P的坐标.
分析 (1)由正方形的性质及点A的坐标得出OC=3,求出x=3时y2的值得出点D的坐标,继而得出反比例函数的解析式;
(2)根据直线和双曲线的解析式求得OF=1、AE=2,从而求得S四边形AOFE=$\frac{9}{2}$,设点P(x,x-1),得出S△POF=$\frac{1}{2}$×1×|x-1|=$\frac{9}{2}$,解之求得x的值,从而求得点P的坐标.
解答 解:(1)∵四边形OABC是正方形,且点A坐标为(0,3),
∴OA=OC=3,
将x=3代入y2=x-1,得:y2=2,
∴点D的坐标为(3,2),
则反比例函数的表达式为y1=$\frac{6}{x}$;
(2)将y=0代入y2=x-1得:x=1,
∴OF=1,
将y=3代入y1=$\frac{6}{x}$,得:x=2,
∴AE=2,
则S四边形AOFE=$\frac{1}{2}$×(1+2)×3=$\frac{9}{2}$,
设点P的坐标为(x,x-1),
则S△POF=$\frac{1}{2}$×1×|x-1|=$\frac{9}{2}$,
解得:x=10或x=-8,
当x=10时,y=9;当x=-8时,y=-9,
∴点P的坐标为(10,9)或(-9,-8).
点评 本题主要考查直线与双曲线的交点问题,熟练掌握待定系数法求函数的解析式及三角形的面积问题是解题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
20.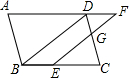 如图,平行四边形ABCD,点E在边BC上,点F在AD边的延长线上,且EF∥BD,EF,CD交于点G,$\frac{DF}{AD}$=$\frac{2}{5}$,S四边形BDGE=a,则S平行四边形ABCD的值为( )
如图,平行四边形ABCD,点E在边BC上,点F在AD边的延长线上,且EF∥BD,EF,CD交于点G,$\frac{DF}{AD}$=$\frac{2}{5}$,S四边形BDGE=a,则S平行四边形ABCD的值为( )
 如图,平行四边形ABCD,点E在边BC上,点F在AD边的延长线上,且EF∥BD,EF,CD交于点G,$\frac{DF}{AD}$=$\frac{2}{5}$,S四边形BDGE=a,则S平行四边形ABCD的值为( )
如图,平行四边形ABCD,点E在边BC上,点F在AD边的延长线上,且EF∥BD,EF,CD交于点G,$\frac{DF}{AD}$=$\frac{2}{5}$,S四边形BDGE=a,则S平行四边形ABCD的值为( )| A. | $\frac{25a}{8}$ | B. | $\frac{25a}{9}$ | C. | $\frac{25a}{16}$ | D. | $\frac{16a}{9}$ |
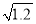 是最简二次根式;
是最简二次根式;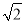 。
。 一慢车和一快车沿相同路线从A地到B地,所行的路程y(千米)与时间x(时)的函数图象如图所示,试根据图象,回答下列问题:
一慢车和一快车沿相同路线从A地到B地,所行的路程y(千米)与时间x(时)的函数图象如图所示,试根据图象,回答下列问题: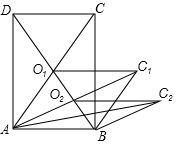 如图所示,矩形ABCD的面积为12cm2,它的两条对角线交于点O1,以AB、AO1邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2;同样以AB、AO2为邻边作平行四边形ABC2O2…;依此类推,则平行四边形ABC6O6的面积为$\frac{3}{16}$cm2.
如图所示,矩形ABCD的面积为12cm2,它的两条对角线交于点O1,以AB、AO1邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2;同样以AB、AO2为邻边作平行四边形ABC2O2…;依此类推,则平行四边形ABC6O6的面积为$\frac{3}{16}$cm2.