题目内容
2.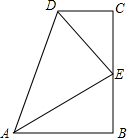 如图所示,在四边形ABCD中,∠B=∠C=90°.E是BC的中点,DE平分∠ADC,∠CED=35°.求∠EAB的度数.
如图所示,在四边形ABCD中,∠B=∠C=90°.E是BC的中点,DE平分∠ADC,∠CED=35°.求∠EAB的度数.
分析 只需延长AB、DE交于点F,然后可证得△CDE≌△BFE,进而由三线合一证得AE与DE是垂直的,最后得出答案.
解答 解:延长DE、AB交于点F,如图,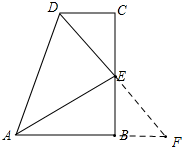
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵∠B=∠C=90°,
∴CD∥AB,
∴∠CDE=∠AFE,
∴∠ADE=∠AFE,
在△CDE和△BFE中,
$\left\{\begin{array}{l}{∠CDE=∠BFE}\\{∠DEC=∠BEF}\\{CE=BE}\end{array}\right.$,
∴△CDE≌△BFE(AAS),
∴DE=EF,
∴AE⊥DF,
∵∠DEC=35°,
∴∠AEB=55°,
∴∠EAB=55°.
点评 本题主要考查了全等三角形的判定与性质、平行线的判定与性质、等腰三角形三线合一的应用、三角形内角和性质,难度中等.注意本题对中点的处理技巧,这可总结为一般方法,即:当出现“平行线夹中点”的情形,通常可构造“X型”全等.

练习册系列答案
相关题目
7.下列各组式子中,为同类项的是( )
| A. | 5x2y与-2xy2 | B. | 3x与3x2 | C. | -2xy与5yx | D. | 4a2b与3a2c |
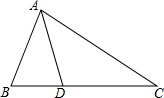 如图,在△ABC中,∠B=2∠C,AD平分∠BAC,AB=$6\sqrt{2}$,BD=$4\sqrt{2}$,则BC=$\frac{32\sqrt{2}}{3}$.
如图,在△ABC中,∠B=2∠C,AD平分∠BAC,AB=$6\sqrt{2}$,BD=$4\sqrt{2}$,则BC=$\frac{32\sqrt{2}}{3}$.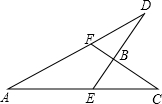 如图,已知∠CBE=96°,∠A=27°,∠C=30°,则∠ADE=27°.
如图,已知∠CBE=96°,∠A=27°,∠C=30°,则∠ADE=27°.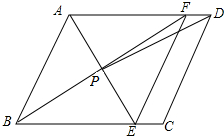 如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD,若AB=4,AD=6,∠ABC=60°,PD的长2$\sqrt{7}$,四边形ABEF的面积8$\sqrt{3}$.
如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD,若AB=4,AD=6,∠ABC=60°,PD的长2$\sqrt{7}$,四边形ABEF的面积8$\sqrt{3}$. 如图,△ABC≌△AED,BC⊥DE,则∠D的度数为45°.
如图,△ABC≌△AED,BC⊥DE,则∠D的度数为45°.