题目内容
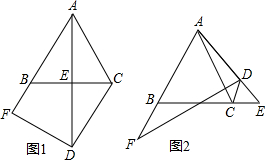
13.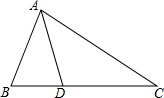 如图,在△ABC中,∠B=2∠C,AD平分∠BAC,AB=$6\sqrt{2}$,BD=$4\sqrt{2}$,则BC=$\frac{32\sqrt{2}}{3}$.
如图,在△ABC中,∠B=2∠C,AD平分∠BAC,AB=$6\sqrt{2}$,BD=$4\sqrt{2}$,则BC=$\frac{32\sqrt{2}}{3}$.
分析 在AC上截取AE=AB=6$\sqrt{2}$,如图所示,利用SAS得到三角形ABD与三角形AED全等,利用全等三角形对应边相等、对应角相等得到DB=DE,∠AED=∠B,利用外角性质等量代换后,再利用等角对等边得到DE=EC,由AE+EC求出AC的长,利用角平分线定理求出DC的长,由BD+DC求出BC的长即可.
解答 解:在AC上截取AE=AB=6$\sqrt{2}$,如图所示,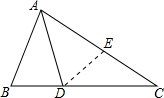
在△ABD和△AED中,
$\left\{\begin{array}{l}{AB=AE}\\{∠BAD=∠EAD}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△AED(SAS),
∴DB=DE=4$\sqrt{2}$,∠AED=∠B=2∠C,
∵∠AED=∠C+∠CDE,
∴∠C=∠CDE,
∴EC=DE=4$\sqrt{2}$,
∴AC=AE+EC=10$\sqrt{2}$,
∵AD平分∠BAC,
∴$\frac{AC}{AB}$=$\frac{CD}{BD}$,即$\frac{10\sqrt{2}}{6\sqrt{2}}$=$\frac{CD}{4\sqrt{2}}$,
解得:CD=$\frac{20\sqrt{2}}{3}$,
则BC=BD+DC=4$\sqrt{2}$+$\frac{20\sqrt{2}}{3}$=$\frac{{32\sqrt{2}}}{3}$,
故答案为:$\frac{32\sqrt{2}}{3}$
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
18.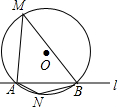 如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
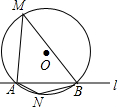 如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 4$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
3. 如图,△ACB≌△A′C′B′,∠BCB′=40°,则∠ACA′的度数为( )
如图,△ACB≌△A′C′B′,∠BCB′=40°,则∠ACA′的度数为( )
 如图,△ACB≌△A′C′B′,∠BCB′=40°,则∠ACA′的度数为( )
如图,△ACB≌△A′C′B′,∠BCB′=40°,则∠ACA′的度数为( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
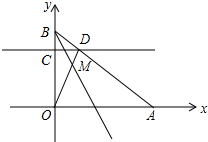 已知,平面直角坐标系中,A(a,0),B(0,b),且a,b满足$\sqrt{a-4}$+|3-b|=0,C点是线段OB上的动点,过C作l∥x轴交AB于点D,连接OD.
已知,平面直角坐标系中,A(a,0),B(0,b),且a,b满足$\sqrt{a-4}$+|3-b|=0,C点是线段OB上的动点,过C作l∥x轴交AB于点D,连接OD. 在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,点E是线段BC上的动点,连AE交CD于点F.
在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,点E是线段BC上的动点,连AE交CD于点F.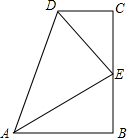 如图所示,在四边形ABCD中,∠B=∠C=90°.E是BC的中点,DE平分∠ADC,∠CED=35°.求∠EAB的度数.
如图所示,在四边形ABCD中,∠B=∠C=90°.E是BC的中点,DE平分∠ADC,∠CED=35°.求∠EAB的度数.