题目内容
17.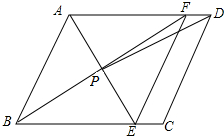 如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD,若AB=4,AD=6,∠ABC=60°,PD的长2$\sqrt{7}$,四边形ABEF的面积8$\sqrt{3}$.
如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD,若AB=4,AD=6,∠ABC=60°,PD的长2$\sqrt{7}$,四边形ABEF的面积8$\sqrt{3}$.
分析 由四边形ABCD是平行四边形,得到AD∥BC,从而得到∠AFB=∠FBE,再由∠ABF=∠FBE,推出∠ABF=∠AFB,于是得到AB=AF,同理得出AB=BE,四边形ABEF是菱形,由菱形的性质得出AE⊥BF,得到∠ABF=30°,∠BAP=∠FAP=60°从而得出AB=AE=4,AP=2,过点P作PM⊥AD于M,得到PM=$\sqrt{3}$,AM=1,从而得到DM=5,由勾股定理求出PD、PB的长,即可得出结果.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AFB=∠FBE,
∵∠ABF=∠FBE,
∴∠ABF=∠AFB,
∴AB=AF,
同理AB=BE,
∴四边形ABEF是菱形,
∴AE⊥BF,
∵∠ABC=60°,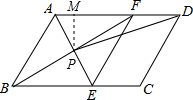
∴∠ABF=30°,∠BAP=∠FAP=60°,△ABE为等边三角形,
∴AB=AE=4,
∵AB=4,
∴AP=2,
过点P作PM⊥AD于M,如图所示:
∴PM=$\sqrt{3}$,AM=1,
∵AD=6,
∴DM=5,
∴PD=$\sqrt{P{M}^{2}+D{M}^{2}}$=$\sqrt{(\sqrt{3})^{2}+{5}^{2}}$=2$\sqrt{7}$;
BP=$\sqrt{A{B}^{2}-A{P}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴菱形ABEF的面积=2×$\frac{1}{2}$BP•AE=2×$\frac{1}{2}$×2$\sqrt{3}$×4=8$\sqrt{3}$;
故答案为:2$\sqrt{7}$,8$\sqrt{3}$.
点评 本题主要考查了平行四边形的性质、平行线的性质、菱形的判定与性质、含30°角的直角三角形性质、勾股定理,等边三角形的判定与性质、菱形面积的计算等知识;熟练掌握菱形的判定与性质是解决问题的关键.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案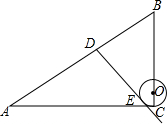 如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,点O为BC上的点,⊙O的半径OC=1,点D是AB边上的动点,过点D作⊙O的一条切线DE(点E为切点),则线段DE的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,点O为BC上的点,⊙O的半径OC=1,点D是AB边上的动点,过点D作⊙O的一条切线DE(点E为切点),则线段DE的最小值为( )| A. | $3\sqrt{2}-1$ | B. | $\sqrt{15}-1$ | C. | $\sqrt{15}$ | D. | 4 |
| A. | 角 | B. | 等边三角形 | C. | 长方形 | D. | 圆 |
 在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,点E是线段BC上的动点,连AE交CD于点F.
在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,点E是线段BC上的动点,连AE交CD于点F.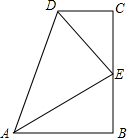 如图所示,在四边形ABCD中,∠B=∠C=90°.E是BC的中点,DE平分∠ADC,∠CED=35°.求∠EAB的度数.
如图所示,在四边形ABCD中,∠B=∠C=90°.E是BC的中点,DE平分∠ADC,∠CED=35°.求∠EAB的度数.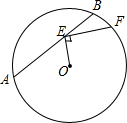 如图,已知⊙O的半径为5,弦AB=8,点E在AB上运动,连结OE,过点E作EF⊥OE交⊙O于点F,当EF最大时,OE+EF的值为7.
如图,已知⊙O的半径为5,弦AB=8,点E在AB上运动,连结OE,过点E作EF⊥OE交⊙O于点F,当EF最大时,OE+EF的值为7.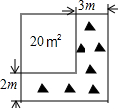 如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,则原正方形空地的边长是( )
如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,则原正方形空地的边长是( )