题目内容
10.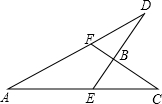 如图,已知∠CBE=96°,∠A=27°,∠C=30°,则∠ADE=27°.
如图,已知∠CBE=96°,∠A=27°,∠C=30°,则∠ADE=27°.
分析 根据三角形的外角性质可知∠DFC=∠A+∠C,再根据对顶角相等以及三角形的内角和性质即可得出∠ADE的度数.
解答 解:∵∠A=27°,∠C=30°,
∴∠DFC=∠A+∠C=57°,
∵∠DBF=∠CBE=96°,
∴∠ADE=180°-∠DFC-∠FBD=180°-57°-96°=27°.
故答案为27°.
点评 本题主要考查了三角形内角和定理以及三角形外角的知识,解答本题的关键是根据三角形外角的性质求出∠DFC的度数,此题难度不大.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
18.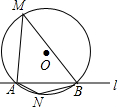 如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
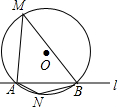 如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 4$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
15.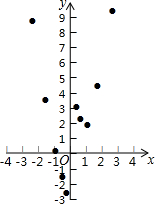 根据学习函数的经验,小明对函数y=x2+$\frac{1}{x}$的图象与性质进行了探究.下面是小明的探究过程,请补充完成:
根据学习函数的经验,小明对函数y=x2+$\frac{1}{x}$的图象与性质进行了探究.下面是小明的探究过程,请补充完成:
(1)函数y=x2+$\frac{1}{x}$的自变量x的取值范围是x≠0.
(2)下表是y与x的几组对应值,其中m=$\frac{28}{3}$;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,2),结合函数的图象,写出该函数的其它性质(一条即可)该函数没有最大值或该函数没有最小值或该函数不经过第四象限或该函数在x=0处断开..
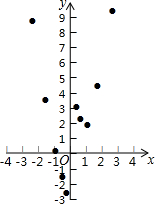 根据学习函数的经验,小明对函数y=x2+$\frac{1}{x}$的图象与性质进行了探究.下面是小明的探究过程,请补充完成:
根据学习函数的经验,小明对函数y=x2+$\frac{1}{x}$的图象与性质进行了探究.下面是小明的探究过程,请补充完成:(1)函数y=x2+$\frac{1}{x}$的自变量x的取值范围是x≠0.
(2)下表是y与x的几组对应值,其中m=$\frac{28}{3}$;
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | $\frac{26}{3}$ | $\frac{7}{2}$ | 0 | -$\frac{7}{4}$ | -$\frac{26}{9}$ | $\frac{28}{9}$ | $\frac{9}{4}$ | 2 | $\frac{9}{2}$ | m | … |
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,2),结合函数的图象,写出该函数的其它性质(一条即可)该函数没有最大值或该函数没有最小值或该函数不经过第四象限或该函数在x=0处断开..
 如图,在平面直角坐标系中,
如图,在平面直角坐标系中,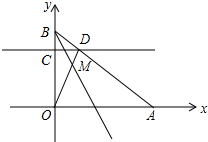 已知,平面直角坐标系中,A(a,0),B(0,b),且a,b满足$\sqrt{a-4}$+|3-b|=0,C点是线段OB上的动点,过C作l∥x轴交AB于点D,连接OD.
已知,平面直角坐标系中,A(a,0),B(0,b),且a,b满足$\sqrt{a-4}$+|3-b|=0,C点是线段OB上的动点,过C作l∥x轴交AB于点D,连接OD. 在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,点E是线段BC上的动点,连AE交CD于点F.
在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,点E是线段BC上的动点,连AE交CD于点F.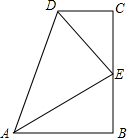 如图所示,在四边形ABCD中,∠B=∠C=90°.E是BC的中点,DE平分∠ADC,∠CED=35°.求∠EAB的度数.
如图所示,在四边形ABCD中,∠B=∠C=90°.E是BC的中点,DE平分∠ADC,∠CED=35°.求∠EAB的度数.