题目内容
12.解下列方程:(1)(x-1)2-4=0;
(2)3x2-2$\sqrt{2}$x=1.
分析 (1)先移项得到(x-1)2=4,然后利用直接开平方法解方程;
(2)先把方程化为一般式,然后利用求根公式法解方程.
解答 解:(1)(x-1)2=4,
x-1=±2,
所以x1=3,x2=-1;
(2)3x2-2$\sqrt{2}$x-1=0,
△=(-2$\sqrt{2}$)2-4×3×(-1)=20,
x=$\frac{2\sqrt{2}±\sqrt{20}}{2×3}$=$\frac{\sqrt{2}±\sqrt{5}}{3}$,
所以x1=$\frac{\sqrt{2}+\sqrt{5}}{3}$,x2=$\frac{\sqrt{2}-\sqrt{5}}{3}$.
点评 本题考查了解一元二次方程-公式法:用求根公式解一元二次方程的方法是公式法.也考查了直接开平方法解一元二次方程.

练习册系列答案
相关题目
3. 如图,△ACB≌△A′C′B′,∠BCB′=40°,则∠ACA′的度数为( )
如图,△ACB≌△A′C′B′,∠BCB′=40°,则∠ACA′的度数为( )
 如图,△ACB≌△A′C′B′,∠BCB′=40°,则∠ACA′的度数为( )
如图,△ACB≌△A′C′B′,∠BCB′=40°,则∠ACA′的度数为( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
20.关于x、y的方程组$\left\{\begin{array}{l}{2x+3y=k}\\{3x+2y=k+2}\end{array}\right.$的解x、y的和为4,则k的值为( )
| A. | 16 | B. | 17 | C. | 9 | D. | 19 |
2. 直线a、b、c、d的位置如图,如果∠1=100°,∠2=100°,∠3=125°,那么∠4等于( )
直线a、b、c、d的位置如图,如果∠1=100°,∠2=100°,∠3=125°,那么∠4等于( )
 直线a、b、c、d的位置如图,如果∠1=100°,∠2=100°,∠3=125°,那么∠4等于( )
直线a、b、c、d的位置如图,如果∠1=100°,∠2=100°,∠3=125°,那么∠4等于( )| A. | 80° | B. | 65° | C. | 60° | D. | 55° |
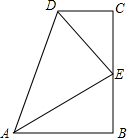 如图所示,在四边形ABCD中,∠B=∠C=90°.E是BC的中点,DE平分∠ADC,∠CED=35°.求∠EAB的度数.
如图所示,在四边形ABCD中,∠B=∠C=90°.E是BC的中点,DE平分∠ADC,∠CED=35°.求∠EAB的度数.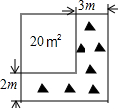 如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,则原正方形空地的边长是( )
如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,则原正方形空地的边长是( )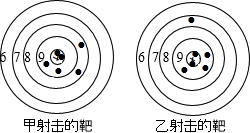 如图是甲乙两人在一次射击比赛中靶的情况(击中靶中心的圆面为10环,靶中数字表示该数所在圆环被击中所得的环数),每人射击了6次.
如图是甲乙两人在一次射击比赛中靶的情况(击中靶中心的圆面为10环,靶中数字表示该数所在圆环被击中所得的环数),每人射击了6次.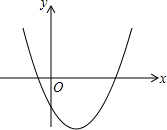 在二次函数y=ax2+bx+c的图象如图所示,下列说法中:①b2-4ac<0;②$-\frac{b}{2a}$>0;③abc>0;④a-b-c>0,说法正确的是②③④(填序号).
在二次函数y=ax2+bx+c的图象如图所示,下列说法中:①b2-4ac<0;②$-\frac{b}{2a}$>0;③abc>0;④a-b-c>0,说法正确的是②③④(填序号). 如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB中点,连接DF、EF,DE、EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:
如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB中点,连接DF、EF,DE、EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论: