题目内容
在△ABC中,D是边BC的中点.
(1)①如图1,求证:△ABD和△ACD的面积相等;
②如图2,延长AD至E,使DE=AD,连结CE,求证:AB=EC.
(2)当∠BAC=90°时,可以结合利用以上各题的结论,解决下列问题:
①求证:AD=
BC(即:直角三角形斜边上的中线等于斜边的一半);
②已知BC=4,将△ABD沿AD所在直线翻折,得到△ADB′,若△ADB′与△ABC重合部分的面积等于△ABC面积的
,请画出图形(草图)并求出AC的长度.
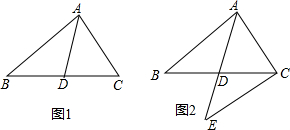
(1)①如图1,求证:△ABD和△ACD的面积相等;
②如图2,延长AD至E,使DE=AD,连结CE,求证:AB=EC.
(2)当∠BAC=90°时,可以结合利用以上各题的结论,解决下列问题:
①求证:AD=
| 1 |
| 2 |
②已知BC=4,将△ABD沿AD所在直线翻折,得到△ADB′,若△ADB′与△ABC重合部分的面积等于△ABC面积的
| 1 |
| 4 |

考点:全等三角形的判定与性质,直角三角形斜边上的中线,翻折变换(折叠问题)
专题:
分析:(1)如图,作辅助线;运用三角形的面积公式即可解决问题;
(2)①证明△ABD≌△ECD,即可解决问题.
②画出图形,运用分类讨论的数学思想,逐一分类解析,即可解决问题.
(2)①证明△ABD≌△ECD,即可解决问题.
②画出图形,运用分类讨论的数学思想,逐一分类解析,即可解决问题.
解答: 解:(1)证明:①过点A作AH⊥BC,垂足为H,
解:(1)证明:①过点A作AH⊥BC,垂足为H,
则S△ABD=
BD•AH,S△ACD=
CD•AH,
∵点D是BC中点,
∴BD=CD,
∴△ABD和△ACD的面积相等.
②在△ABD和△ECD中,
,
∴△ABD≌△ECD(SAS),
∴AB=EC.
(2)①∵△ABD≌△ECD(已证)
∴∠B=∠ECD;
∵∠B+∠ACB=90°,
∴∠ECD+∠ACB=90°,
∴∠ACE=∠BAC=90°;
在△ABC与△CEA中,
,
∴△ABC≌△CEA(SAS),
∴BC=AE;
∵AD=
AE,
∴AD=
BC.
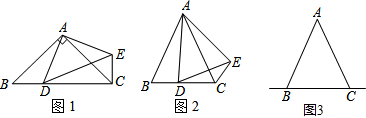
②画草图如下:

(Ⅰ)当AB>AC时,如图3,由△ADB′与△ABC重合部分的面积等于△ABC面积的
,
结合(1)①题的结论,可以得到点O既即是ABˊ的中点,也是CD的中点,
故四边形ADB′C为平行四边形,
∴AC=BˊD=BD=
BC=2.
(Ⅱ)当AB<AC时,
如图4,类比第(Ⅰ)题,同理可证△AOBˊ≌△COD,
∴ABˊ=CD=2,∠Bˊ=∠CDO,
又∵∠Bˊ=∠B,
∴∠B=∠CDO,
∴AB∥OD,
∴∠COD=∠A=90°,
又∵DO=OBˊ=1,
由勾股定理可得CO=
,
∴AC=2CO=2
.
(Ⅲ)当 AB=AC时,由等腰三角形的性质可知,
折叠后重合的面积等于△ABC面积的
,
不可能等于
,所以不合题意,舍去.
综上所述:AC=2或2
.
 解:(1)证明:①过点A作AH⊥BC,垂足为H,
解:(1)证明:①过点A作AH⊥BC,垂足为H,则S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∵点D是BC中点,
∴BD=CD,
∴△ABD和△ACD的面积相等.
②在△ABD和△ECD中,
|
∴△ABD≌△ECD(SAS),
∴AB=EC.
(2)①∵△ABD≌△ECD(已证)
∴∠B=∠ECD;
∵∠B+∠ACB=90°,
∴∠ECD+∠ACB=90°,
∴∠ACE=∠BAC=90°;
在△ABC与△CEA中,
|
∴△ABC≌△CEA(SAS),
∴BC=AE;
∵AD=
| 1 |
| 2 |
∴AD=
| 1 |
| 2 |
②画草图如下:

(Ⅰ)当AB>AC时,如图3,由△ADB′与△ABC重合部分的面积等于△ABC面积的
| 1 |
| 4 |
结合(1)①题的结论,可以得到点O既即是ABˊ的中点,也是CD的中点,
故四边形ADB′C为平行四边形,
∴AC=BˊD=BD=
| 1 |
| 2 |
(Ⅱ)当AB<AC时,
如图4,类比第(Ⅰ)题,同理可证△AOBˊ≌△COD,
∴ABˊ=CD=2,∠Bˊ=∠CDO,
又∵∠Bˊ=∠B,
∴∠B=∠CDO,
∴AB∥OD,
∴∠COD=∠A=90°,
又∵DO=OBˊ=1,
由勾股定理可得CO=
| 3 |
∴AC=2CO=2
| 3 |
(Ⅲ)当 AB=AC时,由等腰三角形的性质可知,
折叠后重合的面积等于△ABC面积的
| 1 |
| 2 |
不可能等于
| 1 |
| 4 |
综上所述:AC=2或2
| 3 |
点评:该题主要考查了直角三角形的性质、全等三角形的判定及其性质的应用等几何知识点问题;牢固掌握全等三角形的判定定理是解题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
下列各组中,是同类项的为( )
A、
| ||||
| B、x2y与x2z | ||||
| C、2mnp与-2mn | ||||
D、-
|
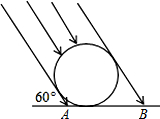 太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上的投影AB的长是12
太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上的投影AB的长是12| 3 |
| A、9cm | ||
| B、18cm | ||
C、6
| ||
D、10
|
 如图,⊙O中,半径OA⊥OE,弦AB交OE于D,过B作⊙O的切线,交OE的延长线于C,若tan∠A=
如图,⊙O中,半径OA⊥OE,弦AB交OE于D,过B作⊙O的切线,交OE的延长线于C,若tan∠A=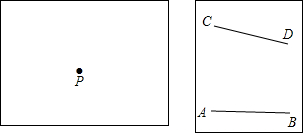 如图,直线AB和CD相交在右边很远的地方,设交点为O,虽然这张纸上画不出我们头脑中想像的∠AOC,但是你能想办法在顶点P处作∠1,使得∠1=∠AOC吗?
如图,直线AB和CD相交在右边很远的地方,设交点为O,虽然这张纸上画不出我们头脑中想像的∠AOC,但是你能想办法在顶点P处作∠1,使得∠1=∠AOC吗? 如图,已知AB∥CD∥EF,若∠1=50°,∠2=150°,求∠3的度数.
如图,已知AB∥CD∥EF,若∠1=50°,∠2=150°,求∠3的度数.