题目内容
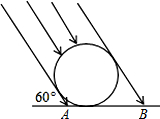 太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上的投影AB的长是12
太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上的投影AB的长是12| 3 |
| A、9cm | ||
| B、18cm | ||
C、6
| ||
D、10
|
考点:切线的性质,平行投影
专题:应用题
分析:太阳光线与⊙O相切于C、D,如图,过A作AE⊥DB于E,连结OC、OD,AB=12
cm,∠ABD=60°,利用切线的性质得OC⊥AC,OD⊥BD,加上AC与BD为平行光线,则OC⊥DB,可判断点C、O、D共线,即CD为⊙O的直径,易得四边形AEDC为矩形,则AE=CD,然后在Rt△ABE中,利用∠ABE的正弦可计算出AE,从而得到圆的直径CD的长.
| 3 |
解答: 解:如图,太阳光线与⊙O相切于C、D,如图,过A作AE⊥DB于E,连结OC、OD,
解:如图,太阳光线与⊙O相切于C、D,如图,过A作AE⊥DB于E,连结OC、OD,
AB=12
cm,∠ABD=60°,
∵太阳光线与⊙O相切于C、D,
∴OC⊥AC,OD⊥BD,
而AC∥BD,
∴OC⊥DB,
∴点C、O、D共线,即CD为⊙O的直径,
∵AE⊥BD,
∴四边形AEDC为矩形,
∴AE=CD,
在Rt△ABE中,∵sin∠ABE=
,
∴AE=12
sin60°=12
×
=18,
∴CD=18,
即皮球的直径长为18cm.
故选B.
 解:如图,太阳光线与⊙O相切于C、D,如图,过A作AE⊥DB于E,连结OC、OD,
解:如图,太阳光线与⊙O相切于C、D,如图,过A作AE⊥DB于E,连结OC、OD,AB=12
| 3 |
∵太阳光线与⊙O相切于C、D,
∴OC⊥AC,OD⊥BD,
而AC∥BD,
∴OC⊥DB,
∴点C、O、D共线,即CD为⊙O的直径,
∵AE⊥BD,
∴四边形AEDC为矩形,
∴AE=CD,
在Rt△ABE中,∵sin∠ABE=
| AE |
| AB |
∴AE=12
| 3 |
| 3 |
| ||
| 2 |
∴CD=18,
即皮球的直径长为18cm.
故选B.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了平行投影.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
下列图形中,对称轴最多的是( )
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
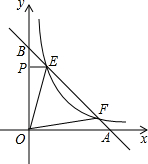 如图,点E,F在函数y=
如图,点E,F在函数y=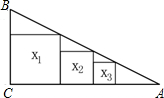 如图,在Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3…,xn的n个正方形依次放入△ABC中,请回答下列问题:
如图,在Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3…,xn的n个正方形依次放入△ABC中,请回答下列问题: 在Rt△ABC中,∠C=90°,b=5,c=5
在Rt△ABC中,∠C=90°,b=5,c=5