题目内容
15.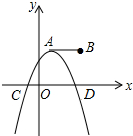 如图,点A,B的坐标分别为(1,3)和(5,3),抛物线y=a(x-h)2+k的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为9.
如图,点A,B的坐标分别为(1,3)和(5,3),抛物线y=a(x-h)2+k的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为9.
分析 当抛物线y=a(x-h)2+k的顶点在线段AB的A点上时,点C的横坐标最小,把A的坐标代入即可求出a的值,因为抛物线y=a(x-h)2+k的顶点在线段AB上运动,所以抛物线的a是定值.根据题意可知当抛物线的顶点运动到B时,D的横坐标最大,把B的坐标和a的值代入即可求出二次函数的解析式,再求出y=0时x的值即可求出答案.
解答 解:当抛物线y=a(x-h)2+k的顶点在线段AB的A点上时,点C的横坐标最小,
把A(1,3)代入得:y=a(x-1)2+3,
把C(-3,0)代入得:0=a(-3-1)2+3,
解得:a=-$\frac{3}{16}$,
即:y=-$\frac{3}{16}$(x-1)2+3,
∵抛物线y=a(x-h)2+k的顶点在线段AB上运动,
∴抛物线的a永远等于-$\frac{3}{16}$,
当抛物线的顶点运动到B时,D的横坐标最大,把a=-$\frac{3}{16}$和顶点B(5,3)代入y=a(x-h)2+k得:y=-$\frac{3}{16}$(x-5)2+3,
当y=0时,0=-$\frac{3}{16}$(x-5)2+3,
解得,x=9或x=1(不合题意,舍去).
所以点D的横坐标最大值为9.
故答案为:9.
点评 本题主要考查了二次函数的性质,用待定系数法求二次函数的解析式,用直接开平方法解一元二次方程等知识点,理解题意并根据已知求二次函数的解析式是解此题的关键,此题是一个比较典型的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知关于x的方程$\frac{1}{4}$x2-(m-2)x+m2=0有两个相等的实数根,则方程的根为( )
| A. | x1=x2=1 | B. | x1=x2=-2 | C. | x1=x2=-1 | D. | x1=x2=2 |
10.小明用17元买了1支笔和某种笔记本3个,已知笔记本的单价比笔的单价的2倍还多1元,设笔每支x元,笔记本每本y元,则所列方程组为( )
| A. | $\left\{\begin{array}{l}{x+3y=17}\\{x=2y+1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+3y=17}\\{y=2x+1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y+3x=17}\\{x=2y+1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y+3x=17}\\{y=2x+1}\end{array}\right.$ |
4.为了打造区域中心城市,实现城市跨越发展,我市新区建设正按投资计划有序进行.新区建设工程部,因道路建设需要开挖土石方,计划每小时挖土石方540m3,现决定向某大型机械租赁公司租甲、乙两种型号的挖掘机来完成这些工作,租赁公司提供的挖掘机有关信息如表:
若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
| 挖掘土石方量(单位:m/台时) | |
| 甲型挖掘机 | 60 |
| 乙型挖掘机 | 80 |
 某洗衣机洗涤衣服时,经历了进水,清洗,排水脱水四个连续的过程,其中进水,清洗,排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如图折线图所示,已知清洗时间为11分钟,排水时间为2分钟,则排水结束时洗衣机中剩下的水量为$\frac{82}{3}$升.
某洗衣机洗涤衣服时,经历了进水,清洗,排水脱水四个连续的过程,其中进水,清洗,排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如图折线图所示,已知清洗时间为11分钟,排水时间为2分钟,则排水结束时洗衣机中剩下的水量为$\frac{82}{3}$升. 如图,为了估计一池塘岸边两点A,B之间的距离,小丽同学在池塘一侧选取了一点P,测得PA=5m,PB=4m,那么点A与点B之间的距离不可能是( )
如图,为了估计一池塘岸边两点A,B之间的距离,小丽同学在池塘一侧选取了一点P,测得PA=5m,PB=4m,那么点A与点B之间的距离不可能是( )