题目内容
6.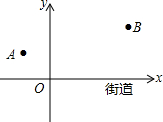 去年“双11”购物节的快递量暴增,某快递公司要在街道旁设立一个派送还点,向A、B两居民区投送快递,派送点应该设在什么地方,才能使它到A、B的距离之和最短?快递员根据实际情况,以街道为x轴,建立了如图所示的平面直角坐标系,测得坐标A(-2,2)、B(6,4),则派送点的坐标是($\frac{2}{3}$,0).
去年“双11”购物节的快递量暴增,某快递公司要在街道旁设立一个派送还点,向A、B两居民区投送快递,派送点应该设在什么地方,才能使它到A、B的距离之和最短?快递员根据实际情况,以街道为x轴,建立了如图所示的平面直角坐标系,测得坐标A(-2,2)、B(6,4),则派送点的坐标是($\frac{2}{3}$,0).
分析 可先找点A关于x轴的对称点C,求得直线BC的解析式,直线BC与x轴的交点就是所求的点.
解答 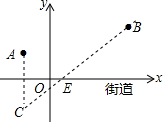 解:作A关于x轴的对称点C,则C的坐标是(-2,-2).
解:作A关于x轴的对称点C,则C的坐标是(-2,-2).
设BC的解析式是y=kx+b,
则$\left\{\begin{array}{l}{-2k+b=-2}\\{6k+b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=-\frac{1}{2}}\end{array}\right.$,
则BC的解析式是y=$\frac{3}{4}$x-$\frac{1}{2}$.
令y=0,解得:x=$\frac{2}{3}$.
则派送点的坐标是($\frac{2}{3}$,0).
故答案是($\frac{2}{3}$,0).
点评 本题考查了对称的性质以及待定系数法求函数的解析式,正确确定派送点的位置是关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
16.一个不透明的袋中装有大小相同的2个红球和2个绿球,如果先从袋中摸出1个球后不放回,再摸出1个球,则两次摸到的球中有个绿球和1个红球的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
1. 如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=40°,则∠EPF的度数是( )
如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=40°,则∠EPF的度数是( )
 如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=40°,则∠EPF的度数是( )
如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=40°,则∠EPF的度数是( )| A. | 25° | B. | 65° | C. | 75° | D. | 85° |
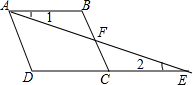 如图,四边形ABCD中,点F是BC中点,连接AF并延长,交于DC的延长线于点E,且∠1=∠2.
如图,四边形ABCD中,点F是BC中点,连接AF并延长,交于DC的延长线于点E,且∠1=∠2.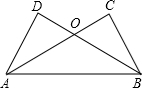 如图,已知AC⊥BC,AD⊥DB,若使△ABC≌△BAD,则还需补充一个条件是AC=BD.
如图,已知AC⊥BC,AD⊥DB,若使△ABC≌△BAD,则还需补充一个条件是AC=BD.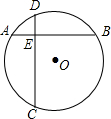 如图,⊙O中弦AB⊥CD于E,AE=2,EB=6,ED=3,则⊙O的半径为$\frac{\sqrt{65}}{2}$.
如图,⊙O中弦AB⊥CD于E,AE=2,EB=6,ED=3,则⊙O的半径为$\frac{\sqrt{65}}{2}$.