题目内容
16.一个不透明的袋中装有大小相同的2个红球和2个绿球,如果先从袋中摸出1个球后不放回,再摸出1个球,则两次摸到的球中有个绿球和1个红球的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
分析 首先根据题意画出树状图或列表,然后由树状图或列表求得所有等可能的结果与两次摸到的球中有个绿球和1个红球的情况,再利用概率公式即可求得答案.
解答 解:
列表如下:
| * | 红1 | 红2 | 绿1 | 绿2 |
| 红1 | * | (红1,红2) | (红1,绿1) | (红1,绿2) |
| 红2 | (红2,红1) | * | (红2,绿1) | (红2,绿2) |
| 绿1 | (绿1,红1) | (绿1,红2) | * | (绿1,绿2) |
| 蓝 | (绿2,红1) | (绿2,红2) | (绿2,绿1) | * |
∴两次摸到的球中有个绿球和1个红球概率为:$\frac{8}{12}$=$\frac{2}{3}$,
故选C.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
7.在△ABC中,AB=AC=5,BC=6,AD平分∠BAC交BC于点D,则BC边上的高线长是( )
| A. | 3 | B. | 3.6 | C. | 4 | D. | 4.8 |
11.在反比例函数y=$\frac{3}{x}$上的一个点是( )
| A. | (1,2) | B. | (1,3) | C. | (2,6) | D. | (0,0) |
 某中学为了预测本校应届毕业女生“一分钟跳绳”项目考试情况,从九年级随机抽取50名女生进行该项目测试,并以测试结果的数据为样本,绘制出如图所示的频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值),已知从左到右各个小长方形的高的比是2:5:8:5:3:2,若测试九年级女生“一分钟跳绳”次数不低于130次的成绩为优秀,这次测试的女生中,成绩优秀的共有20人.
某中学为了预测本校应届毕业女生“一分钟跳绳”项目考试情况,从九年级随机抽取50名女生进行该项目测试,并以测试结果的数据为样本,绘制出如图所示的频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值),已知从左到右各个小长方形的高的比是2:5:8:5:3:2,若测试九年级女生“一分钟跳绳”次数不低于130次的成绩为优秀,这次测试的女生中,成绩优秀的共有20人.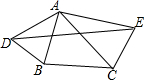 如图,△ABC中,AB=6,AC=8,分别以AB、AC为一边向外作等腰△ADB和等腰△ACE,AD=AB,AE=AC,且∠DAB=∠EAC=x,∠BAC=y(其中2x+y<180°).
如图,△ABC中,AB=6,AC=8,分别以AB、AC为一边向外作等腰△ADB和等腰△ACE,AD=AB,AE=AC,且∠DAB=∠EAC=x,∠BAC=y(其中2x+y<180°).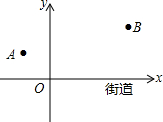 去年“双11”购物节的快递量暴增,某快递公司要在街道旁设立一个派送还点,向A、B两居民区投送快递,派送点应该设在什么地方,才能使它到A、B的距离之和最短?快递员根据实际情况,以街道为x轴,建立了如图所示的平面直角坐标系,测得坐标A(-2,2)、B(6,4),则派送点的坐标是($\frac{2}{3}$,0).
去年“双11”购物节的快递量暴增,某快递公司要在街道旁设立一个派送还点,向A、B两居民区投送快递,派送点应该设在什么地方,才能使它到A、B的距离之和最短?快递员根据实际情况,以街道为x轴,建立了如图所示的平面直角坐标系,测得坐标A(-2,2)、B(6,4),则派送点的坐标是($\frac{2}{3}$,0).