题目内容
17.当x<0时,反比例函数y=-$\frac{3}{x}$中,变量y随x的增大而增大.分析 根据反比例函数的性质:当k<0时,在每一个象限内,函数值y随着自变量x的增大而增大作答.
解答 解:由解析式知k=-3>0,
所以当x<0时,函数y随着自变量x的增大而增大.
故答案为:增大.
点评 本题考查了反比例函数的性质.对于反比例函数y=$\frac{k}{x}$,当k>0时,在每一个象限内,函数值y随自变量x的增大而减小;当k<0时,在每一个象限内,函数值y随自变量x增大而增大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.在△ABC中,AB=AC=5,BC=6,AD平分∠BAC交BC于点D,则BC边上的高线长是( )
| A. | 3 | B. | 3.6 | C. | 4 | D. | 4.8 |
12.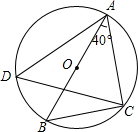 如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )
如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )
 如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )
如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
9.某校七年级全体学生到电影院观看影片.设电影院的座位有x排,若每排坐18人,则有32人无座位;若每排坐20人,则只有8个座位无人坐.下列方程中正确的是( )
| A. | 18x+32=20x-8 | B. | 18x+32=20x+8 | C. | 18x-32=20x-8 | D. | 18x-32=20x+8 |
7.若$\frac{y}{x}=\frac{1}{4}$,则$\frac{x+2y}{x}$的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{2}{3}$ |
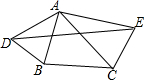 如图,△ABC中,AB=6,AC=8,分别以AB、AC为一边向外作等腰△ADB和等腰△ACE,AD=AB,AE=AC,且∠DAB=∠EAC=x,∠BAC=y(其中2x+y<180°).
如图,△ABC中,AB=6,AC=8,分别以AB、AC为一边向外作等腰△ADB和等腰△ACE,AD=AB,AE=AC,且∠DAB=∠EAC=x,∠BAC=y(其中2x+y<180°).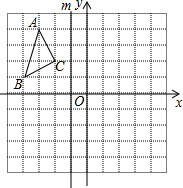 如图所示的正方形网格中,每个小正方形的边长为1,△ABC的三个顶点都在格点上.
如图所示的正方形网格中,每个小正方形的边长为1,△ABC的三个顶点都在格点上.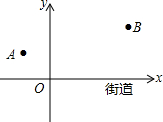 去年“双11”购物节的快递量暴增,某快递公司要在街道旁设立一个派送还点,向A、B两居民区投送快递,派送点应该设在什么地方,才能使它到A、B的距离之和最短?快递员根据实际情况,以街道为x轴,建立了如图所示的平面直角坐标系,测得坐标A(-2,2)、B(6,4),则派送点的坐标是($\frac{2}{3}$,0).
去年“双11”购物节的快递量暴增,某快递公司要在街道旁设立一个派送还点,向A、B两居民区投送快递,派送点应该设在什么地方,才能使它到A、B的距离之和最短?快递员根据实际情况,以街道为x轴,建立了如图所示的平面直角坐标系,测得坐标A(-2,2)、B(6,4),则派送点的坐标是($\frac{2}{3}$,0).