题目内容
6. (1)画出把△ABC沿射线CB方向平移2cm后得到的△A1B1C1;
(1)画出把△ABC沿射线CB方向平移2cm后得到的△A1B1C1;(2)线段AB与线段A1B1有怎么样的关系相等.
分析 (1)根据题意画出△A1B1C1即可;
(2)由图形平移的性质即可得出结论.
解答  解:(1)如图所示;
解:(1)如图所示;
(2)∵△A1B1C1由△ABC平移而成,
∴AB=A1B1.
故答案为:相等.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
相关题目
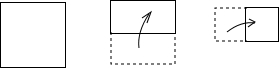
14.将正方形纸片如图所示由下往上对折,再由左向右对折,称为完成一次操作,按上述规则完成三次操作以后,剪去所得小正方形的左下角,问:当展开这张正方形纸片后,小洞孔一共有( )

| A. | 3个 | B. | 4个 | C. | 16个 | D. | 64个 |
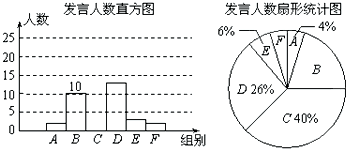
11.某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言的人数比为10:3,请结合图中相关数据回答下列问题:
(1)A组有2人,C组有20人,E组有3人,并补全直方图;
(2)该年级共有学生600人,请估计全年级在这天发言次数不少于20的人数;
(3)已知A组发言的学生中恰有一位女生,E组发言的学生中恰有两位男生,现从A组与E组中分别抽一位学生写报告,求所抽的两位学生至多有一位男生的概率.
| 课堂发言次数n | |
| A | 0≤n<5 |
| B | 5≤n<10 |
| C | 10≤n<15 |
| D | 15≤n<20 |
| E | 20≤n<25 |
| F | 25≤n<30 |
(2)该年级共有学生600人,请估计全年级在这天发言次数不少于20的人数;
(3)已知A组发言的学生中恰有一位女生,E组发言的学生中恰有两位男生,现从A组与E组中分别抽一位学生写报告,求所抽的两位学生至多有一位男生的概率.

18.如果一个不为零的数的平方等于这个数的2倍,那么这个数是( )
| A. | 偶数 | B. | 奇数 | C. | 偶数或奇数 | D. | 不一定是整数 |
16. 如图,∠1=100°,∠A=60°,则∠B的大小是( )
如图,∠1=100°,∠A=60°,则∠B的大小是( )
 如图,∠1=100°,∠A=60°,则∠B的大小是( )
如图,∠1=100°,∠A=60°,则∠B的大小是( )| A. | 10° | B. | 20° | C. | 40° | D. | 80° |
 如图,C为BE上一点,AB=AC,BE=CD.
如图,C为BE上一点,AB=AC,BE=CD.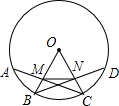 如图,在⊙O中,$\widehat{AB}=\widehat{BC}=\widehat{CD}$,半径OB,OC分别交弦AC,BD于点M,N,求证:∠OMN=∠ONM.
如图,在⊙O中,$\widehat{AB}=\widehat{BC}=\widehat{CD}$,半径OB,OC分别交弦AC,BD于点M,N,求证:∠OMN=∠ONM. 如图,若BD、CD平分∠EBC、∠BCF,交点为D,求证:∠D=90°-$\frac{1}{2}$∠A.
如图,若BD、CD平分∠EBC、∠BCF,交点为D,求证:∠D=90°-$\frac{1}{2}$∠A.