题目内容
18.对于二次函数y=-x2+4x,有下列四个结论:①它的对称轴是直线x=2;②设y1=-x12+4x1,y2=-x22+4x2,则当x2>x1时,有y2>y1;③它的图象与x轴的两个交点是(0,0)和(4,0);④当0<x<4时,y>0.其中正确的结论的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用配方法求出二次函数对称轴,再求出图象与x轴交点坐标,进而结合二次函数性质得出答案.
解答 解:y=-x2+4x=-(x-2)2+4,故①它的对称轴是直线x=2,正确;
②∵直线x=2两旁部分增减性不一样,∴设y1=-x12+4x1,y2=-x22+4x2,则当x2>x1时,有y2>y1或y2<y1,错误;
③当y=0,则x(-x+4)=0,解得:x1=0,x2=4,
故它的图象与x轴的两个交点是(0,0)和(4,0),正确;
④∵a=-1<0,
∴抛物线开口向下,
∵它的图象与x轴的两个交点是(0,0)和(4,0),
∴当0<x<4时,y>0,正确.
故选:C.
点评 此题主要考查了二次函数的性质以及一元二次方程的解法,得出抛物线的对称轴和其交点坐标是解题关键.

练习册系列答案
相关题目
13.一个小球由静止开始在一个斜披上向下滚动,通过一次观察到小球的距离s(m)与时间t(s)的数据如下表所示:
写出用t表示s的函数关系式:s=2t+4.
| t/s | 1 | 2 | 3 | 4 | … |
| s/m | 6 | 8 | 10 | 12 | … |
7. 如图,下列条件中,不能证明△ABC≌△DCB的是( )
如图,下列条件中,不能证明△ABC≌△DCB的是( )
 如图,下列条件中,不能证明△ABC≌△DCB的是( )
如图,下列条件中,不能证明△ABC≌△DCB的是( )| A. | AB=CD,AC=BD | B. | AB=CD,∠ABC=∠BCD | C. | ∠ABC=∠DCB,∠A=∠D | D. | AB=CD,∠A=∠D |
 甲驾车从A地去往B地,到达后停留3个小时,然后返回,往返车速都为120千米/时,乙驾车从B地去往A地,到达后停留1.5小时,因事提前返回,乙往返的车速不变,如图是两车距A地的路程s(千米0与行驶时间t(小时)之间的函数图象,请结合图象回答下列问题:
甲驾车从A地去往B地,到达后停留3个小时,然后返回,往返车速都为120千米/时,乙驾车从B地去往A地,到达后停留1.5小时,因事提前返回,乙往返的车速不变,如图是两车距A地的路程s(千米0与行驶时间t(小时)之间的函数图象,请结合图象回答下列问题: 已知两条直线l1、l2分别经过点A(-1,0)、点B(3,0)并且当两条直线同时相交于y轴的负半轴上的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l1交于点K,与直线l2交于点E,在x轴交于点F,D是抛物线的顶点,如图所示.
已知两条直线l1、l2分别经过点A(-1,0)、点B(3,0)并且当两条直线同时相交于y轴的负半轴上的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l1交于点K,与直线l2交于点E,在x轴交于点F,D是抛物线的顶点,如图所示.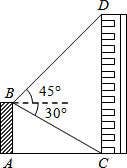 如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,则楼房CD的高度为32.4m.($\sqrt{3}$≈1.7)
如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,则楼房CD的高度为32.4m.($\sqrt{3}$≈1.7)