题目内容
8.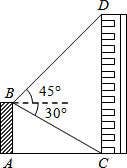 如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,则楼房CD的高度为32.4m.($\sqrt{3}$≈1.7)
如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,则楼房CD的高度为32.4m.($\sqrt{3}$≈1.7)
分析 首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造关系式求解.
解答 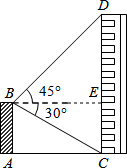 解:如图,过点B作BE⊥CD于点E,
解:如图,过点B作BE⊥CD于点E,
根据题意,∠DBE=45°,∠CBE=30°.
∵AB⊥AC,CD⊥AC,
∴四边形ABEC为矩形.
∴CE=AB=12m.
在Rt△CBE中,cot∠CBE=$\frac{BE}{CE}$,
∴BE=CE•cot30°=12×$\sqrt{3}$=12 $\sqrt{3}$.
在Rt△BDE中,由∠DBE=45°,
得DE=BE=12 $\sqrt{3}$.
∴CD=CE+DE=12( $\sqrt{3}$+1)≈32.4.
答:楼房CD的高度约为32.4m.
故答案为:32.4m.
点评 考查了解直角三角形的应用-仰角俯角问题,本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
19.有下列图形:①线段;②正三角形;③平行四边形;④矩形;⑤圆,既是轴对称图形,又是中心对称图形的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
16. 已知如图,在等边三角形ABC中,若剪去∠B,则图中∠α+∠β等于( )
已知如图,在等边三角形ABC中,若剪去∠B,则图中∠α+∠β等于( )
 已知如图,在等边三角形ABC中,若剪去∠B,则图中∠α+∠β等于( )
已知如图,在等边三角形ABC中,若剪去∠B,则图中∠α+∠β等于( )| A. | 240° | B. | 320° | C. | 180° | D. | 无法计算 |
20.下列计算正确的是( )
| A. | (-3a2)3=-9a6 | B. | (6a6)÷(-3a2)=2a3 | C. | (a-3)2=a2-9 | D. | 4a-5a=-a |
 如图,在△ABC中,∠A=90°,EF∥BC,∠C=40°,则∠1的度数为50°.
如图,在△ABC中,∠A=90°,EF∥BC,∠C=40°,则∠1的度数为50°. 一条排水管的截面如图所示,已知排水管的半径OA=1m,水面宽AB=1.2m,某天下雨后,水管水面上升了0.2m,求此时排水管水面的宽CD.
一条排水管的截面如图所示,已知排水管的半径OA=1m,水面宽AB=1.2m,某天下雨后,水管水面上升了0.2m,求此时排水管水面的宽CD.