题目内容
13.(1)画出函数y=-x-2的图象;(2)判断点A(3,2),B(-1,-1)是否在函数y=-x-2的图象上.
分析 (1)根据一次函数的图象是一条直线,可用两点法画出函数的图象.先求出函数与x、y轴的交点,再描点,连线即可得出函数的图象;
(2)判定A、B是否在函数y=-x-2的图象上,只要将其坐标代入函数中看函数是否成立即可,成立即在函数的图象上,反之不在上面.
解答  解:(1)∵当x=0时,y=-2;当y=0时,x=-2.
解:(1)∵当x=0时,y=-2;当y=0时,x=-2.
∴该直线经过点(0,-2),(-2,0).
其图象如图所示;
(2)∵函数的解析式为y=-x-2,
∴当x=3时,y=-3-2=-5≠2,即A(3,2)不在该函数图象上.
当x=-1时,y=1-2=-1,即点B(-1,-1)在该函数图象上.
点评 此题主要考查了画一次函数图象,以及一次函数图象上点的坐标特点,一次函数的图象的画法:经过两点(0,b)、(-$\frac{b}{k}$,0)或(1,k+b)作直线y=kx+b.

练习册系列答案
相关题目
3.下列说法正确的是( )
| A. | “任意一个三角形的外角和等于180°”这一事件是不可能事件 | |
| B. | 必然事件发生的概率为0 | |
| C. | 一组数据1,6,3,9,8的极差为7 | |
| D. | “面积相等的两个三角形全等”这一事件是必然事件 |
4.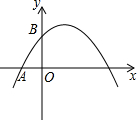 如图,抛物线y=-x2+ax+4与x轴负半轴交于点A,与y轴交于点B,且tan∠ABO=$\frac{1}{4}$,点C(x1,y1),D(x2,y2)是抛物线y=-x2+ax+4上两点,当x1≤x≤x2,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.则下列结论正确的是( )
如图,抛物线y=-x2+ax+4与x轴负半轴交于点A,与y轴交于点B,且tan∠ABO=$\frac{1}{4}$,点C(x1,y1),D(x2,y2)是抛物线y=-x2+ax+4上两点,当x1≤x≤x2,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.则下列结论正确的是( )
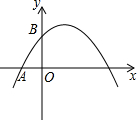 如图,抛物线y=-x2+ax+4与x轴负半轴交于点A,与y轴交于点B,且tan∠ABO=$\frac{1}{4}$,点C(x1,y1),D(x2,y2)是抛物线y=-x2+ax+4上两点,当x1≤x≤x2,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.则下列结论正确的是( )
如图,抛物线y=-x2+ax+4与x轴负半轴交于点A,与y轴交于点B,且tan∠ABO=$\frac{1}{4}$,点C(x1,y1),D(x2,y2)是抛物线y=-x2+ax+4上两点,当x1≤x≤x2,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.则下列结论正确的是( )| A. | a=-3 | B. | y2<4 | C. | |x1-x2|=1 | D. | |x1-$\frac{3}{2}$|>|x2-$\frac{3}{2}$| |
8.下列图形中,∠2>∠1的是( )
| A. |  | B. |  平行四边形 | C. |  | D. |  |
3.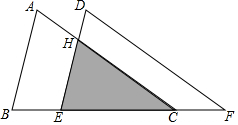 如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=$\sqrt{3}$,则△ABC移动的距离是( )
如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=$\sqrt{3}$,则△ABC移动的距离是( )
 如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=$\sqrt{3}$,则△ABC移动的距离是( )
如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=$\sqrt{3}$,则△ABC移动的距离是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\sqrt{3}$-$\frac{\sqrt{6}}{2}$ |
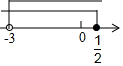


 如图,正方形CEFG的顶点E在?ABCD的AD边上,若∠1=35°,∠2=15°,则∠B的度
如图,正方形CEFG的顶点E在?ABCD的AD边上,若∠1=35°,∠2=15°,则∠B的度 如图,⊙M的圆心M(-1,2),⊙M经过坐标原点O,与y轴交于点A.经过点A的一条直线l解析式为:y=-$\frac{1}{2}$x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(-4,0).
如图,⊙M的圆心M(-1,2),⊙M经过坐标原点O,与y轴交于点A.经过点A的一条直线l解析式为:y=-$\frac{1}{2}$x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(-4,0).